

Published PSMC estimates of Neanderthal effective population size (𝑁e) show an approximately five-fold decline over the past 20,000 years [1]. This observation may be attributed to a true decline in Neanderthal 𝑁e, statistical error that is notorious with PSMC estimation, or geographic subdivision and gene flow that has been hypothesized to occur within the Neanderthal population. Determining which of these factors contributes to the observed decline in Neanderthal 𝑁e is an important question that can provide insight into human evolutionary history.
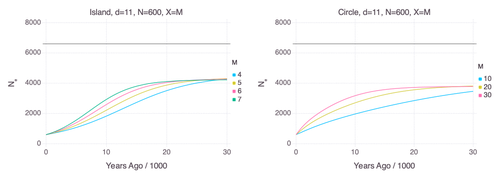
Though it is widely believed that the decline in Neanderthal 𝑁e is due to geographic subdivision and gene flow, no prior studies have theoretically examined whether these evolutionary processes can yield the observed pattern. In this paper [2], Rogers tackles this problem by employing two mathematical models to explore the roles of geographic subdivision and gene flow in the Neanderthal population. Results from both models show that geographic subdivision and gene flow can indeed result in a decline in 𝑁e that mirrors the observed decline estimated from empirical data. In contrast, Rogers argues that neither statistical error in PSMC estimates nor a true decline in 𝑁e are expected to produce the consistent decline in estimated 𝑁e observed across three distinct Neanderthal fossils. Statistical error would likely result in variation among these curves, whereas a true decline in 𝑁e would produce shifted curves due to the different ages of the three Neanderthal fossils.
In summary, Rogers provides convincing evidence that the most reasonable explanation for the observed decline in Neanderthal 𝑁e is geographic subdivision and gene flow. Rogers also provides a basis for understanding this observation, suggesting that 𝑁e declines over time because coalescence times are shorter between more recent ancestors, as they are more likely to be geographic neighbors. Hence, Rogers’ theoretical findings shed light on an interesting aspect of human evolutionary history.
References
[1] Fabrizio Mafessoni, Steffi Grote, Cesare de Filippo, Svante Pääbo (2020) “A high-coverage Neandertal genome from Chagyrskaya Cave”. Proceedings of the National Academy of Sciences USA 117: 15132- 15136. https://doi.org/10.1073/pnas.2004944117
[2] Alan Rogers (2024) “Genetic evidence for geographic structure within the Neanderthal population”. bioRxiv, version 4 peer-reviewed and recommended by Peer Community in Mathematical and Computational Biology. https://doi.org/10.1101/2023.07.28.551046
DOI or URL of the preprint: https://doi.org/10.1101/2023.07.28.551046
Version of the preprint: 3
Both reviewers agreed that the manuscript is well written, clear, and interesting. I am sending this back for revision so that the authors can address some of the minor points that were brought up.
This interesting and nicely written paper explores a potential and actual bias which arises in ancestral demographic estimation when subdivision within the species or population is not accounted for. One way of viewing the bias is as the difference between two ways to describe N_e at some time back in the past.
For the first way, we define N_e(t) to be the rate at time t at which two lineages, sampled at the present, coalesce, conditioned on the lineages not having coalesced previously.
Alternatively, we could define an estimator N_e(t)' which is the rate of coalescence at time t for two lineages sampled at time t. This is the classical (instantaneous) estimator of effective population size.
In a single unsubdivided population, both values are the same.In a subdivided population they can differ since the distribution of the ancestral lineages at time t, conditional on no coalescence, is different than just sampling lineages at time t (say from a stationary distibution). For example, you might expect the two lineages to be in distant demes as you've conditioned on them not having coalesced. You wouldn't expect to sample to genes from a single deme which had gone through a severe bottleneck, for example.
If you run a method like PMSC with a false assumption of no-subdivision then the software will say that it is returning N_e(t)' but actually return N_e(t). This will give a positive bias which increases with t.
The extent of model misspecification bias which arises from this source is determined analytically, and in fact the manuscript is one of the cleanest and clearest derivation of coalescent with migration distributions that I've encountered.
In the end, the conclusion is that the demographic estimates are biased, but not sufficiently to explain the apparent decline in ancestral Neanderthal populations. Nevertheless I could imagine this bias could make a significant impact in other contexts, providing further motivation for explicit modelling of potential subdivisions in this class of analysis
The ms by AR Rogers describes an exploration of parameter space of two simple structure models that were good candidate to explain patterns of Ne(t) variations output by PSMC.I believe the article is sound, well written and very easy to follow.
I thank the author for describing his methodology so clearly and concisely. I think this ms is of interest for population geneticists. The choice of PCI Math Comp Biol is ok but maybe PCI Evol Biol would have been a better target (among the PCIs). I have several suggestions that could potentially improve the overall argument developed here.
1 - it is unclear from the reading how bad is the best possible model. I encourage the author to find a simple way to measure the difference/match between the predictions of the model and the observed data (say distance based or likelihood based). Once the function is computable, it can be optimized. The number of parameters are quite reasonable: d, N, m (or d and M in coalescent time scale).
2- the fact that figure 1 is log-log and Figure 2 log-linear does not help.
3- failing to find parameters that will fit the inferred psmc curve with simple symmetrical model such as the ones studied here hardly demonstrate that no structure model can fit the psmc curve. Having asymmetry in the migration rate, different N per deme, hierarchical structure, etc is also plausible.
4- Equilibrium value of Ne=3600 for archaic humans is not so bizarre (isn't 10^4 for modern human?). The bizarreness stems from the fundamental concept of Ne, that can harbor many disguises, many meanings, many metrics and is often misleading.
In brief, this article is interesting but could be even more stimulating with a larger exploration of models and better inference in their parameter space.
Guillaume Achaz