

 based on reviews by 3 anonymous reviewers
based on reviews by 3 anonymous reviewers
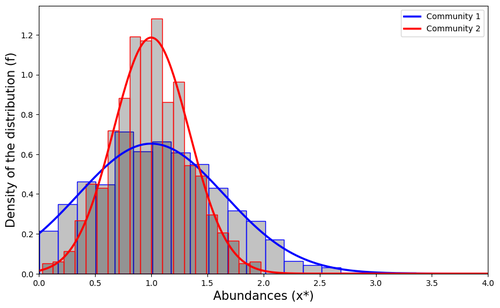
This article by Clenet et al. [1] tackles a fundamental mathematical model in ecology to understand the impact of the architecture of interactions on the equilibrium of the system.
The authors consider the classical Lotka-Volterra model, depicting the effect of interactions between species on their abundances. They focus on the case whenever there are numerous species, and where their interactions are compartmentalized in a block structure. Each block has a strength coefficient, applied to a random Gaussian matrix. This model aims at capturing the structure of interacting communities, with blocks describing the interactions within a community, and other blocks the interactions between communities.
In this general mathematical framework, the authors demonstrate sufficient conditions for the existence and uniqueness of a stable equilibrium, and conditions for which the equilibrium is feasible. Moreover, they derive statistical heuristics for the proportion, mean, and distribution of abundance of surviving species.
While the main text focuses on the case of two interacting communities, the authors provide generalizations to an arbitrary number of blocks in the appendix.
Overall, the article constitutes an original and solid contribution to the study of mathematical models in ecology. It combines mathematical analysis, dynamical system theory, numerical simulations, grounded with relevant hypothesis for the modeling of ecological systems.
The obtained results pave the way to further research, both towards further mathematical proofs on the model analysis, and towards additional model features relevant for ecology, such as spatial aspects.
References
[1] Maxime Clenet, François Massol, Jamal Najim (2023) Impact of a block structure on the Lotka-Volterra model. arXiv, ver.3 peer-reviewed and recommended by Peer Community in Mathematical and Computational Biology. https://doi.org/10.48550/arXiv.2311.09470
DOI or URL of the preprint: https://doi.org/10.48550/arXiv.2311.09470
Version of the preprint: 2
Dear recommender,
We are excited to submit a revised version #2 of our manuscript, ``Impact of a block structure on the Lotka-Volterra model" by Maxime Clenet, François Massol and Jamal Najim. We appreciate the opportunity to improve our manuscript by incorporating the feedback provided by the Reviewers. These revisions have helped us improve the clarity of the manuscript.
Please find the revised manuscript attached, and a detailed point-by-point response to all comments below.
Sincerely,
Maxime Clenet, on behalf of the Authors.
 , posted 10 Aug 2024, validated 12 Aug 2024
, posted 10 Aug 2024, validated 12 Aug 2024Dear authors,
Thank you for your revision. It has been greatly appreciated by the reviewers.
Could you please implement the minor revisions requested, so I can recommend this preprint?
Thanks again,
Best regards,
Loïc Paulevé
I have reviewed the changes. The authors have made the corrections and provided the missing explanation, as requested. I have no further comments. I am now fully satisfied with the new version of the article. I recommend publication of the article.
DOI or URL of the preprint: https://doi.org/10.48550/arXiv.2311.09470
Version of the preprint: 1
Dear recommender,
We are excited to submit a revised version of our manuscript, ``Impact of a block structure on the Lotka-Volterra model" by Maxime Clenet, François Massol and Jamal Najim. We appreciate the opportunity to improve our manuscript by incorporating the feedback provided by the Reviewers. These revisions have helped us improve the clarity of the manuscript.
Please find the revised manuscript attached, and a detailed point-by-point response to all comments below.
Sincerely,
Maxime Clenet, on behalf of the Authors.
 , posted 29 Apr 2024, validated 29 Apr 2024
, posted 29 Apr 2024, validated 29 Apr 2024Dear authors,
Please find enclosed the reviews received for your manuscript. They are all positive, and suggest revisions to strengthen your contribution.
Could you please prepare a new version integrating their corrections and remarks?
Thank you for your submission,
Best regards,
Loïc Paulevé
This paper considered how interactions between two communities impact the existence of unique equilibrium and its stability, and also studied the properties of equilibria. Given a two-community model with interactions captured by a random matrix and strength by a two by two matrix, the authors derived a sufficient condition for the existing of a unique and globally stable equilibrium. They also give sufficient condition for existence of feasible equilibrium.
1. The title reflects the content of the article.
It could be made more precise such as: Impact of a block structure on equilibria of Lotko-Voterra Model
2. Abstract has presented the main results.
3. Introduction is clear and informative
4. Results are well backed by proofs
5. figures are well captioned and labelled.
6. Discussion has given a broader view of the research topic.
7. References are all appropriate.
I am not expert of the topic.