

 based on reviews by 2 anonymous reviewers
based on reviews by 2 anonymous reviewers
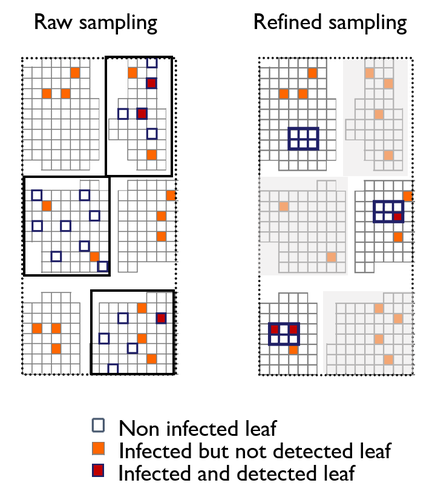
To study the annual invasion of a tree pathogen (Melampsora larici-populina, a fungal species responsible for the poplar rust disease), Xhaard et al (2012) had conducted a spatiotemporal survey along the Durance River valley in the French Alps over nearly 200 km, measuring sampled leaves and twigs from 40 to 150 trees at 12 evenly spaced study sites at seven-time points. By combining Bayesian genetic assignment and a landscape epidemiology approach, they were able to estimate the genetic origin and annual spread of the plant pathogen during a single epidemic.
The observed temporal variation in the spatial pattern of infection rates allowed Saubin et al (2023) to estimate the key factors that determine the speed of the invasion dynamics. In particular, it is crucial to estimate the probability and extent of long-distance dispersal. The dynamics of the macroscale population density was formulated by the reaction-diffusion (R.D.) model and by the integro-difference (I.D.) model. Both consist of the diffusion/dispersal component and the reaction component. In the I.D. model, the kernel function represents the distribution of the dispersion. The likelihood function was obtained by coupling the mathematical model of the population dynamics and the statistical model of the observational process.
Saubin et al (2023) considered a thin-tailed Gaussian kernel, a heavy-tailed exponential kernel, and a fat-tailed exponential power kernel. The numerical simulation reflecting the above survey confirmed the identifiability of the propagation kernel and the accuracy of the parameter estimation. In particular, the above survey had the high power to identify the model with frequent long-distance dispersal. The data from the survey selected the exponential power kernel with confidence. The mean dispersal distance was estimated to be 2.01 km. The exponential power was 0.24. This parameter value predicts that 5% of the dispersals will have a distance > 14.3 km and 1% will have a distance > 36.0 km. The mechanistic-statistical approach presented here may become a new standard for the field-based studies of invasion dynamics.
References
Saubin, M., Coville, J., Xhaard, C., Frey, P., Soubeyrand, S., Halkett, F., and Fabre, F. (2023). A mechanistic-statistical approach to infer dispersal and demography from invasion dynamics, applied to a plant pathogen. bioRxiv, ver. 5 peer-reviewed and recommended by Peer Community in Mathematical and Computational Biology. https://doi.org/10.1101/2023.03.21.533642
Xhaard, C., Barrès, B., Andrieux, A., Bousset, L., Halkett, F., and Frey, P. (2012). Disentangling the genetic origins of a plant pathogen during disease spread using an original molecular epidemiology approach. Molecular Ecology, 21(10):2383-2398. https://doi.org/10.1111/j.1365-294X.2012.05556.x
DOI or URL of the preprint: https://doi.org/10.1101/2023.03.21.533642
Version of the preprint: 4
Dear Managing Board of PCI PCI Math Comp Biol, dear recommender,
We thank the recommender H. Kishino for his careful reading of the manuscript and appendices. There was indeed an error in equations S9 and S10. exp(-uR)* (-uR)^n/n ! should be exp(-uR)* (uR)^n/n ! This error was in the text only.
In the meantime we identified a second error in equation S11 (equation 4 in the main text). This error also occurred in our scripts. We therefore had to rerun all inference and simulation analyses. We apologize for the delays as it took us some time to carry out all theses analyses again.
The results only slightly differ, and for the better. Notably, parameter identifiability was improved, with now correlation coefficients above 0.9 for all parameters and all dispersal models (Table 1). The efficiency of model selection is better when considering the exponential power dispersal kernel, and the confidence (delta AIC) also increased (Table 2). The model best supported by the data describing the epidemics of poplar rust along the Durance River valley is still the exponential power dispersal kernel (Table 3). The estimated values are very similar with on average less than 6% difference (Table 4).
We hope that in its revised state, the manuscript will be suitable for recommendation in PCI Mathematical and Computational Biology.
Yours sincerely,
Méline Saubin (on behalf of all co-authors)
 , posted 26 Sep 2023, validated 28 Sep 2023
, posted 26 Sep 2023, validated 28 Sep 2023Dear Dr. Saubin,
I am willing to write a letter of recommendation for your submitted manuscript.
Before doing so, I would like to ask you to confirm that
exp(-uR)* (-uR)^n/n! in Eqs. S9 and S10
should be
exp(-uR)* (uR)^n/n! .
In light of your reply, I will submit the recommendation.
Sincerely yours,
Hiro
DOI or URL of the preprint: https://doi.org/10.1101/2023.03.21.533642
Version of the preprint: 2
 , posted 05 Jul 2023, validated 06 Jul 2023
, posted 05 Jul 2023, validated 06 Jul 2023Dear Dr. Méline Saubin,
We received two reviews of your preprint entitled ' A mechanistic-statistical approach to infer dispersal and demography from invasion dynamics, applied to a plant pathogen'. Both appreciate the work and provide a few comments, which may be answered appropriately. I would also encourage the authors to add a set of figures which show the predicted values by the four models. By contrasting it with Figure 3 and describing the cause of insufficient fit of the other models, the manuscript may become even more persuasive for general readers.
Sincerely yours,
Hirohisa Kishino
Comments by Reviewer 1
I declare that I have no conflict of interest with the authors or the content of the article
Anonymously
Review as text
This article proposes a mechanistic-statistical approach to model dispersal events. The article is original, well-written and interesting.
I have few comments to help to clarify few points:
You propose two models: RD is based on diffusion while ID is based on kernel. Can you discuss the pro and the con of both models (especially from an applied point of view)?
Your kernel is described for $\tau<1$, $\tau=1$ and $\tau=2$. What happens when $\tau>1$ (and not equal to 2)?
In your raw sampling, you consider a tree as a group of independent leaves. This assumption seems strong. Did I miss something?
AIC is often conservative in terms of model selection. Did you try some alternative such as BIC?
Based on your simulations, I have the impression that your model is particularly efficient for fat-tail exponential power kernel and has a low power for the other cases. Fortunately, it corresponds to you application and the expected value of $\tau$ is low enough. It makes sense since you will not have sufficient data for long range dispersal for thin-tail kernel. Can you discuss this point?
Comments by Reviewer 2
I declare that I have no conflict of interest with the authors or the content of the article
Anonymously
Review as text
This is a well written paper, and the topic of the paper is clearly important. A strength of the paper is that the code and data are available, so that the reader can reproduce (I have not tried) or modify the analysis.
Comments and questions:
What are the assumptions about the random effects Ri(t)? Are they independent between two timepoints t1 and t2, but what if t1 and t2 are close?
One weakness of the approach (seen from my perspective), is that the initial condition u0(x) needs to be specified. Multiple initial conditions were used to test sensitivity, and the results were found to be insensitive to the choice of u0. However, in other situations, the conclusion may be different, and hence making the approach less attractive.
The authors use a derivative free optimizer to maximize the likelihood function, but I wonder why they did not use automatic differentiation to calculate derivatives. This would have had several benefits: 1) speed up, and make more numerically stable, the optimization process, 2) yield exact sensitivities wrt to u0, 3) allow inclusion of (parts of) u0 among the parameters that are estimated. A software package such as TMB (Kristensen et al., 2016) can calculate the first and second order derivatives of the log-likelihood. The requirement for this to work is that the likelihood is differentiable (not containing if-statements that depend on parameter values), and I have not verified if this is the case here.
To put the approach in a broader context it would have been nice to include a comparison with space-time latent Gaussian random field (LGRF) (Lindgren et al., 2011) as an alternative to the mechanistic model. I am not in a position to request that the author actually do this in their paper, but it would nice to have a discussion of the merits of the two approaches. An advantage of the LGRF is that it would automatically estimate u0.
Minor comments:
1. I was able to extract this material from the Zenodo repository., but not from the gitlab repository, which at the time of trying was “private”.
2. Line 88: should be “the true organism’s dispersal process”
3. Line 101: Missing space before reference
4. Line 624, 662: “Mechanistic‐Statistical”
References:
Kristensen, Kasper, et al. "TMB: Automatic Differentiation and Laplace Approximation." Journal of Statistical Software 70 (2016): 1-21.
Lindgren, Finn, Håvard Rue, and Johan Lindström. "An explicit link between Gaussian fields and Gaussian Markov random fields: the stochastic partial differential equation approach." Journal of the Royal Statistical Society Series B: Statistical Methodology 73.4 (2011): 423-498.
This article proposes a mechanistic-statistical approach to model dispersal events. The article is original, well-written and interesting.
I have few comments to help to clarify few points :
You propose two models : RD is based on diffusion while ID is based on kernel. Can you discuss the pro and the con of both models (especially from an applied point of view)
Your kernel is described for $\tau<1$, $\tau=1$ and $\tau=2$. What happen when $\tau>1$ (and not equal to 2)
In your raw sampling, you consider a tree as a group of independent leaves. This assumption seems strong. Dis I miss something ?
AIC is often conservative in terms of model selection. Did you try some alternative such as BIC ?
Based on your simulations, I have the impression that your model is particularly efficient for fat-tail exponential power kernel and has a low power for the other cases. Fortunatly, it corresponds to you application and the expected value of $\tau$ is low enough. It make sens since you will not have sufficient data for long range dispersal for thin-tail kernel. Can you discuss this point
This is a well written paper, and the topic of the paper is clearly important. A strength of the paper is that the code and data are available, so that the reader can reproduce (I have not tried) or modify the analysis.
Comments and questions:
What is the assumptions about the random effects Ri(t)? Are they independent between two timepoints t1 and t2, but what if t1 and t2 are close?
One weakness of the approach (seen from my perspective), is that the initial condition u0(x) needs to be specified. Multiple initial conditions were used to test sensitivity, and the results were found to be insensitive to the choice of u0. However, in other situations, the conclusion may be different, and hence making the approach less attractive.
The authors use a derivative free optimizer to maximize the likelihood function, but I wonder why they did not use automatic differentiation to calculate derivatives. This would have had several benefits: 1) speed up, and make more numerically stable, the optimization process, 2) yield exact sensitivities wrt to u0, 3) allow inclusion of (parts of) u0 among the parameters that are estimated. A software package such as TMB (Kristensen et al., 2016) can calculate the first and second order derivatives of the log-likelihood. The requirement for this to work is that the likelihood is differentiable (not containing if-statements that depend on parameter values), and I have not verified if this is the case here.
To put the approach in a broader context it would have been nice to include a comparison with space-time latent Gaussian random field (LGRF) (Lindgren et al., 2011) as an alternative to the mechanistic model. I am not in a position to request that the author actually do this in their paper, but it would nice to have a discussion of the merits of the two approaches. An advantage of the LGRF is that it would automatically estimate u0.
Minor comments:
1. I was able to extract this material from the Zenodo repository., but not from the gitlab repository, which at the time of trying was “private”.
2. Line 88: should be “the true organism’s dispersal process”
3. Line 101: Missing space before reference
4. Line 624, 662: “Mechanistic‐Statistical”
References:
Kristensen, Kasper, et al. "TMB: Automatic Differentiation and Laplace Approximation." Journal of Statistical Software 70 (2016): 1-21.
Lindgren, Finn, Håvard Rue, and Johan Lindström. "An explicit link between Gaussian fields and Gaussian Markov random fields: the stochastic partial differential equation approach." Journal of the Royal Statistical Society Series B: Statistical Methodology 73.4 (2011): 423-498.