
A new perspective in modeling mutation rate for phenotypically structured populations
The emergence of a birth-dependent mutation rate in asexuals: causes and consequences
Abstract
Recommendation: posted 07 December 2021, validated 07 December 2021
Lou, Y. (2021) A new perspective in modeling mutation rate for phenotypically structured populations . Peer Community in Mathematical and Computational Biology, 100006. https://doi.org/10.24072/pci.mcb.100006
Recommendation
In standard mutation-selection models for describing the dynamics of phenotypically structured populations, it is often assumed that the mutation rate is constant across the phenotypes. In particular, this assumption leads to a constant diffusion coefficient for diffusion approximation models (Perthame, 2007 and references therein).
Patout et al (2021) study the dependence of the mutation rate on the birth rate, by introducing some diffusion approximations at the population level, derived from the large population limit of a stochastic, individual-based model. The reaction-diffusion model in this article is of the “cross-diffusion” type: The form of “cross-diffusion” also appeared in ecological literature as a type of biased movement behaviors for organisms (Shigesada et al., 1979). The key underlying assumption for “cross-diffusion” is that the transition probability at the individual level depends solely upon the condition at the departure point. Patout et al (2021) envision that a higher birth rate yields more mutations per unit of time. One of their motivations is that during cancer development, the mutation rates of cancer cells at the population level could be correlated with reproduction success.
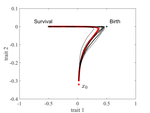
The reaction-diffusion approximation model derived in this article illustrates several interesting phenomena: For the time evolution situation, their model predicts different solution trajectories under various assumptions on the fitness function, e.g. the trajectory could initially move towards the birth optimum but eventually end up at the survival optimum. Their model also predicts that the mean fitness could be flat for some period of time, which might provide another alternative to explain observed data. At the steady-state level, their model suggests that the populations are more concentrated around the survival optimum, which agrees with the evolution of the time-dependent solution trajectories.
Perhaps one of the most interesting contributions of the study of Patout et al (2021) is to give us a new perspective to model the mutation rate in phenotypically structured populations and subsequently, and to help us better understand the connection between mutation and selection. More broadly, this article offers some new insights into the evolutionary dynamics of phenotypically structured populations, along with potential implications in empirical studies.
References
Perthame B (2007) Transport Equations in Biology Frontiers in Mathematics. Birkhäuser, Basel. https://doi.org/10.1007/978-3-7643-7842-4_2
Patout F, Forien R, Alfaro M, Papaïx J, Roques L (2021) The emergence of a birth-dependent mutation rate in asexuals: causes and consequences. bioRxiv, 2021.06.11.448026, ver. 3 peer-reviewed and recommended by Peer Community in Mathematical and Computational Biology. https://doi.org/10.1101/2021.06.11.448026
Shigesada N, Kawasaki K, Teramoto E (1979) Spatial segregation of interacting species. Journal of Theoretical Biology, 79, 83–99. https://doi.org/10.1016/0022-5193(79)90258-3
The recommender in charge of the evaluation of the article and the reviewers declared that they have no conflict of interest (as defined in the code of conduct of PCI) with the authors or with the content of the article. The authors declared that they comply with the PCI rule of having no financial conflicts of interest in relation to the content of the article.
Reviewed by Hirohisa Kishino , 12 Nov 2021
, 12 Nov 2021
The authors responded to the reviewers' comments well in the revised manuscript.
https://doi.org/10.24072/pci.mcb.100006.rev21Reviewed by anonymous reviewer 1, 02 Nov 2021
The authors have addressed all my concerns. I am happy to recommend acceptance of this paper by PCI.
https://doi.org/10.24072/pci.mcb.100006.rev22Evaluation round #1
DOI or URL of the preprint: https://doi.org/10.1101/2021.06.11.448026
Version of the preprint: 1
Author's Reply, 30 Oct 2021
Decision by Yuan Lou, posted 16 Sep 2021
This paper studies the dependence of the mutation rate on the birth rate by introducing some diffusion approximations at the population level, derived from the large population limit of a stochastic, individual based model. The reaction-diffusion model is of the “cross-diffusion” type: the form of “cross-diffusion” also appeared in earlier ecological literatures as a type of biased movement behaviors; see, e.g. the work of Shigesada et al. (TPB 1979). There are two key underlying assumptions of “cross-diffusion”: first, the transition probability depends only upon the condition at the departure point; second, increasing the diffusion rate has the tendency to move more individuals away from the departure location. In current work the authors envision that a higher birth rate yield more mutations per unit time at the population level.
Their reaction-diffusion model illustrates several interesting phenomena: for the time evolution situation, their model predicts different solution trajectories under various assumptions on the fitness function, e.g. the trajectory could initially move towards the birth optimum but eventually end up at the survival optimum. Their model also predicts that the mean fitness could be flat for some period of time, which might provide another alternative to explain observed data. At the steady state level, their model suggests that the populations are more concentrated around the survival optimum, which agrees with the evolution of the time-dependent solution trajectories.
Probably one of the most interesting implications of the work is to give the readers a new view to model the mutation rate and subsequently, to understand the intricate connection between mutation and selection, and more broadly, to gain new insights into the evolutionary dynamics.
Both reports are positive and enthusiastic. I concur with the reviewers and recommend that the paper could be recommended after revision. The reviewers made some suggestions/comments, which need to be addressed.
Reviewed by anonymous reviewer 1, 03 Aug 2021
The effect of mutation and selection on the phenotypic distribution has a long history. In most previous models, the rate of mutation was assumed to be the same across all phenotypes. However, biologically speaking the rate of mutation should be proportional to the appeareance of birth events. In particular, phenotypes with higher birth rate necessarily have higher mutation rates, even if the probability of mutation is the same for each birth event.
This article has two main parts. The first part concerns the derivation of continuum models as limits of discrete individual based models, with focus on determining which conditions on the discrete models can lead to the standard continuum model (where mutation does is independent of phenotype) and which conditions lead to the new continuum model. This parts is based on improving upon the work of Champagnat at el.. This provides concrete conditions for which the new models applies.
The second part concerns the numerical results elucidating new phenomenon found in the new continuum model that is not observed in the standard model. The authors designed the numerical investigation in the following way. Suppose the phenotypic variable x is one dimensional, and the fitness is given by b(x) - d(x), where b(x) and d(x) are the birth and death rates as functions of x. Assume that b(x) and d(x) are unimodel functions, while b(x) - d(x) are bimodal with equal maximum values attained at two points x1 and x2. While the fitness is equal at both x1 and x2 (i.e. b(x1)-d(x1)=b(x2)-d(x2)), the two points are distinguished by the fact that b(x1) > b(x2). In this case, the numerical results demonstrates that the mean phenotype first move towards the birth optimum x1, where it plateaus for some amount of time, before eventually settles near the survival optimum x2. This stands in contrast with the standard model in which the population does not distinguish the two fitness optimum points x1 and x2.
The authors explains the above new phenomenon as follows. While both x1 and x2 are evolutionary attractors, mutation toward x1 is enhanced when the population is far away from both x1 and x2, due to the asymmetry of the mutation kernel. Hence, the bulk of the population evolve towards a neighborhood of x1. However, if we split the population into the group in neighborhood of x1 and in neighborhood of x2, then the first group has slightly lower fitness comparing with the latter group, since higher mutation means the variance is greater among the first group. This difference in mutation is small, so it takes a longer timescale before the second group dominates eventually.
I find the article well written and interesting. While the mathematical analysis is not new per se, the author has identified a question well motivated by biology, and provided new results (new continuum model) and insights (new phenomenon and mechanistic reasons) using analytical as well as numerical methods. I recommend acceptance of this article.
Comments:
P.5, The coupling <\nu, \phi> is not well-defined in general if \nu is a measure and \phi is only assumed to be bounded measurable. I suggest to restrict \phi to continuous functions here.
P.5, Is f_t uniquely determined by (5)? If so, please state it in the Proposition 2.1 with appropriate references. The same comments applies for Propositions 2.3 and 2.4.
P.6, 1st line, "if f_0 is absolutely continuous with respect to the Lebesgue measure,...."
P.13, the last paragraph. I think the explanation for the initial bias to the right is well written. Can you give more detail to the explanation for the other case when the initial bias is to the left? Does this has to do with the monotonicity of the eigenvalue perhaps?
P.14. It seems to be that there are two different mechanisms at work -- the most dominant force is the fitness gradient, which forces the population to move towards x1 and x2 (and nowhere else). When the population is away from x1, x2, the two fitness optimal is roughtly the same, so the mutation assymmetry takes the population towards x1. When the population is concentrated in a neighborhood of \{x1,x2\}, the model becomes one of competition between two distinct population, in which the population around x2 wins by virtue of a smaller variance (or the monotonicity of eigenvalue).
Typos:
P.4, 5th line below (Q_b): "However, not always,..." to "However, this is not always the case, ...."
P.6, line 8, "mutant individuals appear at a higher rate" to "mutation occurs at a higher rate". (Since mutation individuals is not well defined.
P.6, line 9, "as we shall expose below" to "as we shall explain below"
P.6, line 9, "wide ranging consequences" to "far reaching consequences"
P.7, in the assumption (SE), the second appearance of \rho should be replaced by \rho_K.
https://doi.org/10.24072/pci.mcb.100107.rev11










