
Faster method for estimating the openness of species
Revisiting pangenome openness with k-mers
Abstract
Recommendation: posted 10 April 2024, validated 10 April 2024
van Iersel, L. (2024) Faster method for estimating the openness of species. Peer Community in Mathematical and Computational Biology, 100185. https://doi.org/10.24072/pci.mcb.100185
Recommendation
When sequencing more and more genomes of a species (or a group of closely related species), a natural question to ask is how quickly the total number of distinct sequences grows as a function of the total number of sequenced genomes. A similar question can be asked about the number of distinct genes or the number of distinct k-mers (length-k subsequences).
The paper “Revisiting pangenome openness with k-mers” [1] describes a general mathematical framework that can be applied to each of these versions. A genome is abstractly seen as a set of “items” and a species as a set of genomes. The question then is how fast the function f_tot, the average size of the union of m genomes of the species, grows as a function of m. Basically, the faster the growth the more “open” the species is. More precisely, the function f_tot can be described by a power law plus a constant and the openness $\alpha$ refers to one minus the exponent $\gamma$ of the power law.
With these definitions one can make a distinction between “open” genomes ($\alpha < 1$) where the total size f_tot tends to infinity and “closed” genomes ($\alpha > 1$) where the total size f_tot tends to a constant. However, performing this classification is difficult in practice and the relevance of such a disjunction is debatable. Hence, the authors of the current paper focus on estimating the openness parameter $\alpha$.
The definition of openness given in the paper was suggested by one of the reviewers and fixes a problem with a previous definition (in which it was mathematically impossible for a pangenome to be closed).
While the framework is very general, the authors apply it by using k-mers to estimate pangenome openness. This is an innovative approach because, even though k-mers are used frequently in pangenomics, they had not been used before to estimate openness. One major advantage of using k-mers is that it can be applied directly to data consisting of sequencing reads, without the need for preprocessing. In addition, k-mers also cover non-coding regions of the genomes which is in particular relevant when studying openness of eukaryotic species.
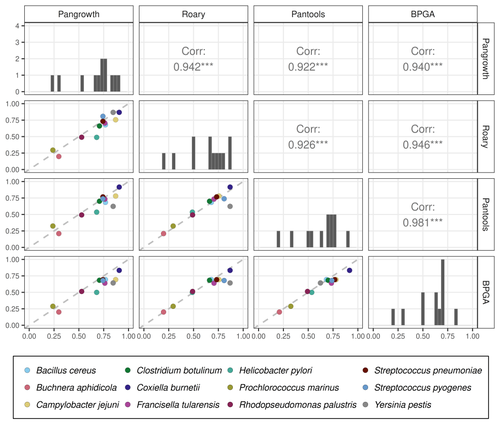
The method is evaluated on 12 bacterial pangenomes with impressive results. The estimated openness is very close to the results of several gene-based tools (Roary, Pantools and BPGA) but the running time is much better: it is one to three orders of magnitude faster than the other methods.
Another appealing aspect of the method is that it computes the function f_tot exactly using a method that was known in the ecology literature but had not been noticed in the pangenomics field. The openness is then estimated by fitting a power law function.
Finally, the paper [1] offers a clear presentation of the problem, the approach and the results, with nice examples using real data.
References
[1] Parmigiani L., Wittler, R. and Stoye, J. (2024) "Revisiting pangenome openness with k-mers". bioRxiv, ver. 4 peer-reviewed and recommended by Peer Community In Mathematical and Computational Biology. https://doi.org/10.1101/2022.11.15.516472
The recommender in charge of the evaluation of the article and the reviewers declared that they have no conflict of interest (as defined in the code of conduct of PCI) with the authors or with the content of the article. The authors declared that they comply with the PCI rule of having no financial conflicts of interest in relation to the content of the article.
This project received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 956229. It was also supported by the BMBF-funded de.NBI Cloud within the German Network for Bioinformatics Infrastructure (de.NBI) (031A532B, 031A533A, 031A533B, 031A534A, 031A535A, 031A537A, 031A537B, 031A537C, 031A537D, 031A538A)
Reviewed by Guillaume Marçais, 22 Feb 2024
The authors have addressed my remaining major comments: 1) fixed the mathematical definition of open / closed genomes and 2) added a discussion on examples of closed genomes.
I have no further comments.
https://doi.org/10.24072/pci.mcb.100185.rev31Evaluation round #2
DOI or URL of the preprint: https://doi.org/10.1101/2022.11.15.516472
Version of the preprint: 3
Author's Reply, 20 Feb 2024
Decision by Leo van Iersel, posted 12 Oct 2023, validated 12 Oct 2023
The authors did a very good job incorporating most comments of the riviewers. Unfortunately, the main comment has not yet been resolved sufficiently. Although I do believe that the added text has improved the paper, I agree with the reviewer that more work needs to be done.
For example, in the introduction you state that "one of the most outstanding discoveries at the time was that some species possess an open pangenome and others a closed pangenome" but then you use a model in which it is impossible for a pangenome to be closed.
The other remaining problem is that you test your method only on open pangenomes. Of course this makes sense because it cannot work for closed pangenomes, but then this weakness of the method should at least be stated clearly.
The reviewer gives a very nice suggestion for how to resolve these issues. I recommend to follow this suggestion if possible.
Reviewed by Guillaume Marçais, 21 Sep 2023
Reviewed by anonymous reviewer 1, 23 Aug 2023
I support this article Accept
https://doi.org/10.24072/pci.mcb.100185.rev22Evaluation round #1
DOI or URL of the preprint: https://doi.org/10.1101/2022.11.15.516472
Version of the preprint: 2
Author's Reply, 17 Aug 2023
Decision by Leo van Iersel, posted 10 May 2023, validated 15 May 2023
The problem and approach I find very interesting, but the reviewers have a number of important questions that need to be answered first. Most importantly, please:
- justify the used definitions of open/closed genomes and explain the practical relevance of the results based on this definition;
- make the supplementary figures and tables available;
- explain why the blue line in Figure 1 does not fit the data;
- analyse how the practical running time depends on the number of samples;
- analyse the distribution of alpha values in the experiments;
- explain why the method was compared only to Roary and Pantools.
Reviewed by Guillaume Marçais, 07 Feb 2023
In "Revisiting pangenome openness with k-mers" the authors give a computational
method and an implementation to estimate how "open" a pan-genome is, that is
whether the genome of a species has many variant genes (opened) or is more
constrained (closed). This is traditionally done by comparing gene content of
different individual bacteria of a species, but is done here using k-mer content
instead.
Although the proposed computational method seem correct, the definition of
open/close pan-genome raises questions. Consequently the conclusions drawn from
the experiments are affected by the flaw in the definition.
Major comments
==============
* Page 4, line 153: it is stated that 0 <= \gamma <= 1 and \alpha = 1 - \gamma
(hence 0 <= \alpha <= 1 as well). Then line 158, the definition of a close
genome is for \alpha > 1, which cannot happen by definition. A close genome
would imply \gamma < 0, that is the number of k-mer seen would be a decreasing
function of m (m = number of genomes considered). This simply cannot be observed.
Unsurprisingly, all the values reported by the proposed method (see Fig. 4)
have an \alpha < 1 and are all declared to be open genomes. That is not an
empirical conclusion based on data, but a mathematical guarantee independent
of the data.
* The Supplementary material does not seem to be available, even though it
contains important figures.
* Fig 1 page 5: the fitting of the blue line does not seem to match the data.
The conclusion that \alpha = 0.98 for this data set is questionable. It seems
like this data does not follow Heaps' law. Maybe the fact that this data does
not follow Heaps' law is the signature of a closed genome?
Minor comments
==============
* The use of GMP to compute f_{tot} is not well justified. The ratio (n-i)^{m} /
n^{m} (where ^{m} is the falling factorial as in the text) probably doesn't
need an infinite precision library. It is the product of the ratios
(n-i-j)/(n-j) for 0 <= j < m. These ratios and their product can most likely
be stored in double floats without significant loss in precision (and is
likely cheaper to compute).
* There is no timing or memory usage information given for the bacterial
experiments.
* GNU should be capitalized (it is an accronym)
* Page 9, line 274: "making k-mers more suitable" is ambiguous. k-mers are more
suitable for bacterial genomes or eukariotic genomes?
Reviewed by anonymous reviewer 1, 09 May 2023
Parmigiani et al. used k-mers to estimate pan-genome openness. It's a nice idea, but also challenging work. I have some small questions:
1) Based on the different numbers of samples (10, 20, 50, 100), what is the running time of this algorithm?
2) The author tested twelve bacterial species, how many strains were tested for each species?
3) In addition to Roary and Pantools, should it be compared with other software?
Reviewed by Abiola Akinnubi, 14 Apr 2023
The mathematical equation were well explained and it was articulated. I endorse this and say it should be accepted.
Thank you
https://doi.org/10.24072/pci.mcb.100185.rev13










