
VAN IERSEL Leo
- Delft Institute of Applied Mathematics, Delft University of Technology, Delft, Netherlands
- Combinatorics, Computational complexity, Design and analysis of algorithms, Evolutionary Biology, Graph theory, Machine learning
- recommender
Recommendation: 1
Reviews: 0
Recommendation: 1
Revisiting pangenome openness with k-mers
Faster method for estimating the openness of species
Recommended by Leo van Iersel based on reviews by Guillaume Marçais, Abiola Akinnubi and 1 anonymous reviewerWhen sequencing more and more genomes of a species (or a group of closely related species), a natural question to ask is how quickly the total number of distinct sequences grows as a function of the total number of sequenced genomes. A similar question can be asked about the number of distinct genes or the number of distinct k-mers (length-k subsequences).
The paper “Revisiting pangenome openness with k-mers” [1] describes a general mathematical framework that can be applied to each of these versions. A genome is abstractly seen as a set of “items” and a species as a set of genomes. The question then is how fast the function f_tot, the average size of the union of m genomes of the species, grows as a function of m. Basically, the faster the growth the more “open” the species is. More precisely, the function f_tot can be described by a power law plus a constant and the openness $\alpha$ refers to one minus the exponent $\gamma$ of the power law.
With these definitions one can make a distinction between “open” genomes ($\alpha < 1$) where the total size f_tot tends to infinity and “closed” genomes ($\alpha > 1$) where the total size f_tot tends to a constant. However, performing this classification is difficult in practice and the relevance of such a disjunction is debatable. Hence, the authors of the current paper focus on estimating the openness parameter $\alpha$.
The definition of openness given in the paper was suggested by one of the reviewers and fixes a problem with a previous definition (in which it was mathematically impossible for a pangenome to be closed).
While the framework is very general, the authors apply it by using k-mers to estimate pangenome openness. This is an innovative approach because, even though k-mers are used frequently in pangenomics, they had not been used before to estimate openness. One major advantage of using k-mers is that it can be applied directly to data consisting of sequencing reads, without the need for preprocessing. In addition, k-mers also cover non-coding regions of the genomes which is in particular relevant when studying openness of eukaryotic species.
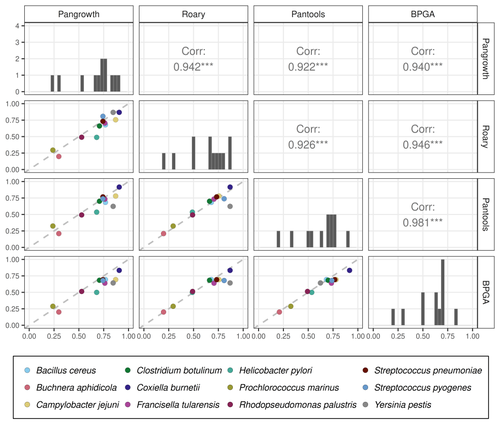
The method is evaluated on 12 bacterial pangenomes with impressive results. The estimated openness is very close to the results of several gene-based tools (Roary, Pantools and BPGA) but the running time is much better: it is one to three orders of magnitude faster than the other methods.
Another appealing aspect of the method is that it computes the function f_tot exactly using a method that was known in the ecology literature but had not been noticed in the pangenomics field. The openness is then estimated by fitting a power law function.
Finally, the paper [1] offers a clear presentation of the problem, the approach and the results, with nice examples using real data.
References
[1] Parmigiani L., Wittler, R. and Stoye, J. (2024) "Revisiting pangenome openness with k-mers". bioRxiv, ver. 4 peer-reviewed and recommended by Peer Community In Mathematical and Computational Biology. https://doi.org/10.1101/2022.11.15.516472