Dear authors,

Thanks a lot for your revision and the care you brought to addressing all the comments by the reviewers and myself.

It took me much longer than expected to hand my decision, because each time I resumed reading the manuscript, it was slown down by some paragraph I had hard times grasping.

I am really close to recommending your nice paper, but I would appreciate your improving clarity by addressing the following (virtually all minor) points:

- line 97 “if antibiotic treatment is started early by the human host before pathogenic bacteria have reached the resource limits of their niche, our model could be approximately accurate.” I am not sure a model can be ‘accurate’ and I don’t think anything can be ‘approximately accurate’, please reformulate

- lines 85 and 100-101: can you specify that total resistance is equivalent to E_{M_A} (C_A) = E_{M_B} (C_B) = 0, which is basically equivalent to z_AA and z_BB infinite?

- lines 107-110, I understand your reasoning concerning the gates AND and OR, but I am not sure I am convinced by their translation in terms of birth and death rates. I think I can understand (in terms of competing exponential clocks) that it is equivalent to assume that the effects of drugs on death rate are summed and to say that ‘it is sufficient for either drug to cause its death’. But it does not seem equivalent (to me) to assume that the effects of drugs on division rate are multiplied and to say that ‘for a cell to divide both pathways impacted by the drugs must remain functional’. 

- line 123 `to make evolving this stochastic system computationally feasible’: I’m not sure it is the right way to justify using tau-leaping – the system is really simple to simulate with a classical Doob-Gillespie algorithm. It’s more that you speed up simulations this way.  

- line 136, z_{S,A} and z_{S,B} are specified, but nothing is said of the 4 other z’s. Also please give the units of \mu and \delta.

- lines 147-149, ‘The more important point for this simple theoretical model is to use parameter values that highlight biologically relevant phenomena, rather than using maximally likely parameter values’. I’m not sure to see what you mean. What are parameter values that ‘highlight biologically relevant phenomena’ if these parameter values are not ‘likely’? Do you mean parameter values do not need to be finely tuned, but only need to be in the right ballpark?

- line 171, you should explain the link between gambler’s ruin and probability of extinction (or just explain that (7) can be obtained directly by saying that extinction does occur iff at each division event, we don't have both a mutation event and the survival of this mutant)

- line 216, what do you mean by ‘directionally plausible’?

- Equation 14, I’m not sure the three dots (forming a triangle) are canonical to symbolize logical implication

- line 226, ‘if only A or B is used’, please add ‘that is, if C_A or C_B is zero’… (makes more clearly the link with the previous case when C_A=C_B)

- line 228, alternative formulation: ‘the survival probability of a mutant is more sensitive to an increase in concentration of the drug to which resistance mutations arise more frequently’

- Equation 15, I agree it is nice to have this relationship between C_A/C_B and \mu_A/\mu_B, however, this formulation does not highlight the dependence on C of the result, and suggests that there is a degree of freedom in the choice of C_A and C_B. It would be clearer to first state that at the optimal combination, we have C_A = C/(1+\sqrt{\mu_A/\mu_B }) and C_B = C\sqrt{\mu_A/\mu_B }/(1+\sqrt{\mu_A/\mu_B})

- The paragraph starting line 259 is somewhat obscure to me. We read that ‘As resistance becomes weaker (from the earlier unrealistic supposition of total resistance), the two resistant strains become less perfectly adapted to their respective drugs’, which means that E_{M_A} (C_A) and E_{M_B} (C_B) should be nonzero. It would be good to say that now z_{M_A, A} and z_{M_B, B} are finite (otherwise it is difficult to make the link with the case of total resistance). Also please change the caption of Figure 2 and S1, which only mentions z_{M_A, B} and z_{M_B, A}. We read that these two values are exponentially distributed with expectation \zeta, but it is not exactly true, they’re equal to 1+ an exponential rv with expectation \zeta -1: this implies that they are always larger than 1; please explain why (I guess you want M_A to be more resistant to B than S, but this is not straightforward for the reader and this should maybe be justified biologically?). 

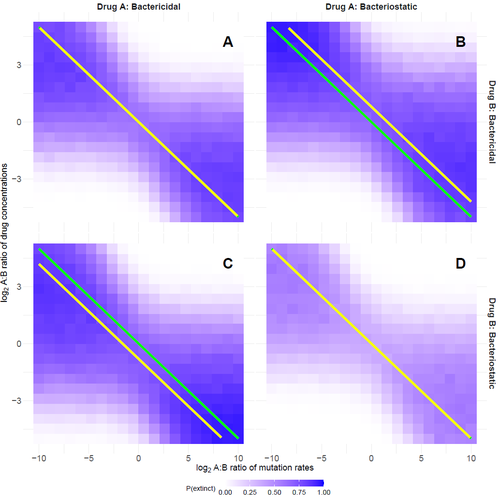
- Figure 1, please specify that the yellow and green lines are confounded in panels A and D (yellow is not visible). It is surprising that the yellow curve of optimal dosing is always so straight (there is no reason why it should be a line a priori) and even confounded with the green line in panel A: are you sure there is no mathematical result available when the drugs are not necessarily bacteriostatic? (see also comment by Reviewer 1 in 1st round) 

- lines 295-304, can you be more specific about how you model cost? Otherwise, it is difficult to understand/believe your quite clear-cut conclusion that ‘too intermediate dosing strategies are sufficient to ensure P_E ≈ 1 even for very skewed mutation rates’.

- line 318, ‘This suggests that ignoring pharmacokinetics (as in the analytical solution) is not a fatal flaw’. Please reformulate.

- line 319, ‘Each replication event uses one arbitrary unit of resource, and the simulation begins with 10^9 units of resource, with a constant influx of 10^8 h−1. The maximum growth rate is now given by the Monod equation, with a resource affinity constant of 10^8’. Can you expand a little bit the paragraph starting here, explain your modeling assumptions, give symbols to these parameters (units, influx and affinity of resource), provide an equation for the effect on growth rate, explain your choice of parameter values and give an idea about how your results are robust or not to these choices? You say that ‘the basic relationship between mutation rate and optimal dosing concentrations persists’ but without a yellow curve, what we see is mainly the negative relationship between C_A/C_B and \mu_A/\mu_B, which is expected.

- line 333, ‘less beneficial’ => more hazardous/risky

- line 338 ‘but in several cases the dosing skew should never be raised above some maximum value.’ I must have missed something, can you specify which of your findings you are referring to here?

- line 351, ‘Our choices of functional forms for the drug-dependent mortality and replication rates in Equations 2 and 3 were crucial for the results that followed.’ Are you speaking of the mathematical results? Otherwise, it is a little worrying that these choices are crucial.

- line 366, ‘As a result, unlike with Bliss independence, skewed drug dosing ratios do not clear the infection slower.’ It is not clear to me how you conclude this from the previous considerations

- line 373, ‘in reality, there is no sharp cutoff’, please recall here why your assumption that the total drug dose is smaller than c can be seen as a cutoff

- line 408-409, if you want to interpret mutations in your model as HGT, you have to consider the rate of HGT within a host; under mass-action, the (per susceptible pathogenic bacterial cell) rate should be proportional to R, where R is the number of (commensal) bacteria carrying the resistance gene already present within the host, which itself depends in a nonlinear and time-dependent manner on the number, denoted I in this paragraph, of hosts ‘infected’ by this bacteria (see also comment by Reviewer 1 in 1st round). I understand that this rate is somewhat external to the dynamics you are studying, and does not interfere with it, but you should be a little more cautious when you say that it is approximately constant – it is at least time-dependent.

- line 414-415, ‘Thus, using a drug to which the commensal bacteria is susceptible could make resistance considerably less likely to evolve.’ You’re basically saying that due to possible HGT, it is better to use a drug for which there are no resistance genes already present in the microbial community. I’m not sure this is worth saying. 

- Figures S3-S4: please say a word in main text or caption how to interpret the Z-shaped yellow curves. In Figures 3 and S2, you explain that beyond a certain threshold value of mutation rate ratio, the best strategy is to use only one drug. But what’s happening in Figures S3 and S4?

Please be so kind as to prepare a revised version of your manuscript addressing these points,

Best,

Amaury Lambert

Dear authors,

Let me first apologize for the delay in handing this decision - I have come through a very difficult summer at a personal level.

The two referees have written reports of high quality. They appreciated the manuscript but have a number of important comments that you are asked to address in your revision. A few points in particular have retained my attention:

- You have made a noticeable effort in relaxing some simplifying assumptions, except for one which seems particularly important. In the manuscript, the growth rates of bacterial populations are always constant - there is neither competition between populations nor time inhomogeneity due to drug elimination (see comments by Referee 1). Please assess the domain of validity of your results in relation to (at least one of) these assumptions. This point seems to be addressed in another preprint of yours cited in the manuscript. Since both manuscripts are rather short, you might consider merging them, as proposed by Referee 2.

- Please be more diligent in citing and comparing your work with existing literature on the topic of antibiotic resistance evolution (e.g., works cited by Referee 2). Also please provide more references from the "significant body of empirical literature" on combination therapy (line 28).

- You could easily address several comments of both referees, and at the same time improve clarity, by expanding a little bit your presentation of the model and of the consequences of your simplifying assumptions regarding parameter values :

    - First, assuming that the beta's and the phi's are all equal to 1, G_S = g/((1+C_A)(1+C_B)). Then your assumption that S and M_B both have zero net growth rate when C_A = 0 and C_B = c implies g = \delta (1+c) and G_A = g/(1+C_B) (similarly with M_B). You should also say that under these assumptions, whenever C_A+C_B=c, G_S<D_S and G_A>D_A (similarly with M_B);

    - Second, you should write the calculations that lead to (13) and emphasize in particular (see comment by Referee 1) the intermediate step showing that (up to the dividing factor 1+c) you have that \mu(1-P_D) = \mu_A C_A + \mu_B C_B and that (the expectation of) N_r = S_0/(C_A C_B).

Minor points:

- The division (or birth) rate of bacterial cells is called growth rate and denoted G. It is more common to define the growth rate as the difference between birth and death rate.

- Note that (11) can be obtained directly by saying that extinction does occur iff at each division event, we don't have both a mutation event and the survival of this mutant;

- Note that because you assume that the exponential decrease of S is deterministic, you have that: 1) N_r has a Poisson distribution with parameter given by the rhs of (8); 2) because N_r is a Poisson variable, equation (12) holds without approximation by taking the expectation of (11) (wrt the law of N_r), which results in (12) after replacing N_r with its expectation (i.e., the parameter of its law).

Please prepare a revised version of your manuscript addressing these points and and the points raised by the two referees.

Best,

Amaury Lambert