
Towards accurate inference of insect presence landscapes from pheromone sensor networks
 based on reviews by Angelo Iollo and 1 anonymous reviewer
based on reviews by Angelo Iollo and 1 anonymous reviewer
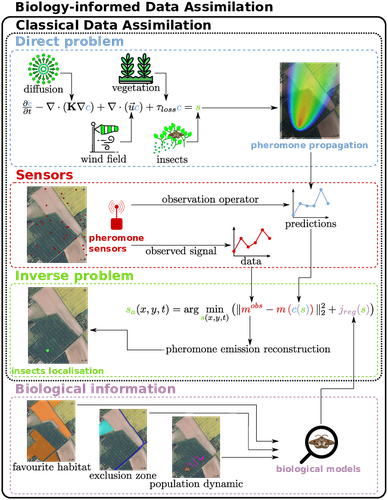
Biology-Informed inverse problems for insect pests detection using pheromone sensors
Abstract
Recommendation: posted 25 January 2025, validated 27 January 2025
Tannier, E. (2025) Towards accurate inference of insect presence landscapes from pheromone sensor networks. Peer Community in Mathematical and Computational Biology, 100313. https://doi.org/10.24072/pci.mcb.100313
Recommendation
Insecticides are used to control crop pests and prevent severe crop losses. They are also a major cause of the current decline in biodiversity, contribute to climate change, and pollute soil and water, with consequences for human and environmental health [1]. The rationale behind the work of Malou et al [2] is that some pesticide application protocols can be improved by a better knowledge of the insects, their biology, their ecology and their real-time infestation dynamics in the fields. Thanks to a network of pheromone sensors and a mathematical method to derive the spatio-temporal distribution of pest populations from the signals, it is theoretically possible to adjust the time, dose and area of treatment and to use less pesticide with greater efficiency than an uninformed protocol.
Malou et al [2] focus on the mathematical problem, recognising that its real role in pest control would require work on its implementation and on a benefit-harm analysis. The problem is an "inverse problem" [3] in that it consists of inferring the presence of insects from the trail left by the pheromones, given a model of pheromone diffusion by insects. The main contribution of this work is the formulation and comparison of different regularisation terms in the optimisation inference scheme, in order to guide the optimisation by biological knowledge of specific pests, such as some parameters of population dynamics.
The accuracy and precision of the results are tested and compared on a simple toy example to test the ability of the model and algorithm to detect the source of the pheromones and the efficiency of the data assimilation principle. A further simulation is then carried out on a real plot with realistic parameters and rules based on knowledge of a maize pest. A repositioning of the sensors (informed by the results from the initial positions) is carried out during the test phase to allow better detection.
The work of Malou et al [2] is large, deep and complete. Its includes a detailed study of the numerical solutions of different data assimilation methods, as well as a theoretical reflection on how this work could contribute to agricultural and environmental issues.
References
[1] IPBES (2024). Thematic Assessment Report on the Underlying Causes of Biodiversity Loss and the Determinants of Transformative Change and Options for Achieving the 2050 Vision for Biodiversity of the Intergovernmental Science-Policy Platform on Biodiversity and Ecosystem Services. O’Brien, K., Garibaldi, L., and Agrawal, A. (eds.). IPBES secretariat, Bonn, Germany. https://doi.org/10.5281/zenodo.11382215
[2] Thibault Malou, Nicolas Parisey, Katarzyna Adamczyk-Chauvat, Elisabeta Vergu, Béatrice Laroche, Paul-Andre Calatayud, Philippe Lucas, Simon Labarthe (2025) Biology-Informed inverse problems for insect pests detection using pheromone sensors. HAL, ver.2 peer-reviewed and recommended by PCI Math Comp Biol https://hal.inrae.fr/hal-04572831v2
[3] Isakov V (2017). Inverse Problems for Partial Differential Equations. Vol. 127. Applied Mathematical Sciences. Cham: Springer International Publishing. https://doi.org/10.1007/978-3-319-51658-5.
The recommender in charge of the evaluation of the article and the reviewers declared that they have no conflict of interest (as defined in the code of conduct of PCI) with the authors or with the content of the article. The authors declared that they comply with the PCI rule of having no financial conflicts of interest in relation to the content of the article.
The authors acknowledge the support of the French National Research Agency (ANR) under the grant ANR-20-PCPA-0007 (PheroSensor).
Evaluation round #1
DOI or URL of the preprint: https://hal.inrae.fr/hal-04572831
Version of the preprint: 1
Author's Reply, 14 Jan 2025
Decision by Eric Tannier , posted 27 Oct 2024, validated 27 Oct 2024
, posted 27 Oct 2024, validated 27 Oct 2024
The submitted paper proposes a data assimilation framework for an inverse problem. The inverse problem consists in predicting an insect presence landscape given a network of pheromone sensors and a pheromone diffusion model. The data assimilation framework consists in using the control term of the inverse problem to guide the optimisation by some biological knowledge of specific pests, such as some parameters of population dynamics (BI-DA).
The motivation is a more rational use of pesticides than prophylaxis or less informed models.
The accuracy and precision of the results are tested on a simple toy example to test the ability of the model and the algorithm to detect the source of the pheromones and the efficiency of the BI-DA principle. A further simulation is then carried out on a real plot with realistic parameters and regulations based on knowledge of a maize pest. A repositioning of the sensors (informed by the data of the initial positions) is carried out during the test phase to allow a better detection.
The paper has been well evaluated by two referees who, based on their comments, propose to ask for a revision. Their comments should be useful to improve the paper and should not imply major changes.
I also have a list of suggestions, which are not mandatory and should be considered as a guide to improve the paper if the authors find them relevant.
Suggestions:
- The introduction could be improved by some minor clarifications of the motivation. From line 44, it is argued that the use of pesticides when pests are detected could be an economy compared to prophylaxis, and implicitly that knowing the location of insects can lead to additional economies. Is it because pesticides are used less frequently (only when pests are detected), or because they are used in smaller quantities (based on an estimate of a population size), or because they can only be used in parts of fields where insects are detected? Are there empirical studies showing that the use of sensors actually leads to less pesticide use than prophylaxis, and that the use of more precise insect positions through inverse problems leads to less pesticide use than the presence/absence signal from sensors?
- The mathematical model deals with the concentration of a particular pheromone, specific to a particular insect. The introduction says that the sensors can detect many different types of pheromone. So is there one model per insect species? When used in the field, are there many models running in parallel? What is the typical number of models?
- The running time of the optimisation could be compared with the insects' breeding time to know if the real time application is feasible.
- I did not understand part 3.4.4 and the statement that some sensors could be removed. I understood that this means knowing the location of the insects, or at least the signal from the sensors, but how can they be removed if this is unknown a priori? Besides this point, a sensitivity test on the number of sensors would be informative, did you choose the number of sensors in the test with an intuition of an optimal number?
- I sometimes got lost in the description of the results for the toy example test. It is long, has a lot of information and I hardly got the most important ones (like "in most cases the "all-reg" performs better than the "no reg""). From this part I got the impression that BI-DA has little effect and that this depends strongly on the combination of the regulations, together with some parameters of the simulation. If I am wrong, there should be a sentence summarising the results. As the article is quite long, you might consider shortening this part.
- The use of sensor repositioning would be mentioned in the introduction or in the methods. It seems important for the understanding of the results and seems both a drawback of the method (if real repositioning is needed in the field) and a methodological contribution (although you admit in the conclusion that it is beyond this work).
- The description of the results of the FAW test case is also very long, describing some tiny details of the figure and missing an interpretation message.
- As the classical data assimilation (DA) problem seems to be ill-conditioned and allows to reconstruct the
the amount of pheromone emitted in the vicinity of the sensors, we propose" → I did not understand this sentence: does "ill-conditioned" have a definition? Why "seems" and not "is"? I did not see the articulation.
- In the discussion you mention a possible multiple repositioning of sensors, but I don't understand how this can be related to reality in a field. Is it possible to change the position of sensors several times during a pest invasion?
- I wonder how much the conclusions depend on the specific design of the test cases. Some parameters have been arbitrarily fixed, do you have any intuition about the robustness of the conclusions to other types of designs?
- I also wondered about the distance of such a study from the application that motivates it. What would be the next steps towards realising the economic proposition?
- I also wondered about the amount of computation needed to make the predictions, the pressure on resources to do it, and whether the balance of benefits and risks was so clearly in favour of using it to reduce pesticides.
Possible typos:
- insect pheromones are specie-specific → species-specific?
- the same homogeneous diffusion tensor than the toy case is used → than in the toy case? Or as in the toy case?
- In a first time we optimize → As a first step?
- improves a little → slightly improve?
- how a specific sensor impact → impacts
- no insect were correctly located → no insect was?
- that are not consider → considered?
- following the following steps → using the following steps?
Reviewed by anonymous reviewer 1, 29 Jul 2024
The paper entitled: Biology-informed inverse problems for insect pests detection using pheromone sensors deals with a source estimation problem for a reaction-difusion-advection model in the context of insect invasion in agriculture. The setup is a standard Variational formulation for the source detection inverse problem. The main contribution consists in adding regularisation terms which enforce weakly (by penalisation) some expected behaviours. The paper is well written and presents a valuable contribution. It deserves publication after a revision. Please, find hereafter some comments and questions.
1) The 2d model of reaction-diffusion type is well justified in appendix B. In this model, the wind velocity is assumed to be constant in the x,y direction and negligible in the z direction. This motivates the fact that, in the z direction, the passive scalar falls due to gravity.
It is assumed that u,v are near to average over the layer of interest. This could be a first reasonable assumption (depending on the size, in z, of the layer of interest). However, it is neglecting the ground boundary layer, which makes the components u,v to be depending on z. Could the authors:
a) comment on the size in z of the layer of interest
b) comment on this modelling assumption and on the impact it could have on the results?
2) In the model, it is assumed that the initial concentration is zero. Is this modelling assumption justified? Could the authors comment on this point?
3) One of the main contributions of the paper consists in adding biology-informed regularisation terms. These consist in penalising the discrepancy with respect to some expected behaviour. Concerning the term in 3.1.3:
a) it is a PDE residual based on a population dynamics model. What are the conditions for the residual to be in L^2?
b) Is the residual penalised in strong form? What about the boundary conditions for this model?
4) The authors discuss about the fact that the noise could induce negative source values, which are unphysical. Could a constraint of positive source be enforced?
5) In the discussion, several sources of uncertainty are described. Could the authors prospect on the possibility of performing Uncertainty Quantification and estimate the impact of the uncertainties on the results?
Reviewed by Angelo Iollo, 15 Oct 2024
The work is rich in content, rigorous, well-argued, and the numerical examples are well-documented. The main contribution lies in the formulation and comparison of different regularization terms for a data assimilation problem. The article undoubtedly deserves to be published. However, the authors could consider the following points, which may help clarify certain aspects:
1. If I understand correctly, the control problem is posed in infinite dimensions, meaning that the number of degrees of freedom increase as the grid is refined. However, it is not clear which specific control variables are actually used and what the dimension of the control space is in the applied cases.
2. In relation to point 1. it might be useful to precondition the search space to avoid infinite dimensionality, which could introduce high-frequency spatial instabilities and reduce the convergence rate.
3. The authors emphasize that they use a gradient of the discrete problem. It would be interesting to show the validation of this gradient, for example, by comparing it to finite differences. Additionally, it would be helpful to demonstrate the convergence rate of the optimization problem as well as the norm of the gradient in both applicative cases.
4. The proposed technique is based on a posteriori approach. It could be useful in applications to periodically update the source predictions based on newly acquired measurements, as done in 4DVAR in meteorology.
5. How does this approach compare with standard state observers like Kalman filters?
https://doi.org/10.24072/pci.mcb.100313.rev12










