
Disclosing effects of Boolean network reduction on dynamical properties and control strategies
Phenotype control and elimination of variables in Boolean networks
Abstract
Recommendation: posted 09 August 2024, validated 13 August 2024
Chaouiya, C. (2024) Disclosing effects of Boolean network reduction on dynamical properties and control strategies. Peer Community in Mathematical and Computational Biology, 100318. 10.24072/pci.mcb.100318
Recommendation
Boolean networks stem from seminal work by M. Sugita [1], S. Kauffman [2] and R. Thomas [3] over half a century ago. Since then, a very active field of research has been developed, leading to theoretical advances accompanied by a wealth of work on modelling genetic and signalling networks involved in a wide range of cellular processes. Boolean networks provide a successful formalism for the mathematical modelling of biological processes, with a qualitative abstraction particularly well adapted to handle the modelling of processes for which precise, quantitative data is barely available. Nevertheless, these abstract models reveal fundamental dynamical properties, such as the existence and reachability of attractors, which embody stable cellular responses (e.g. differentiated states). Analysing these properties still faces serious computational complexity. Reduction of model size was proposed as a mean to cope with this issue. Furthermore, to enhance the capacity of Boolean networks to produce relevant predictions, formal methods have been developed to systematically identify control strategies enforcing desired behaviours.
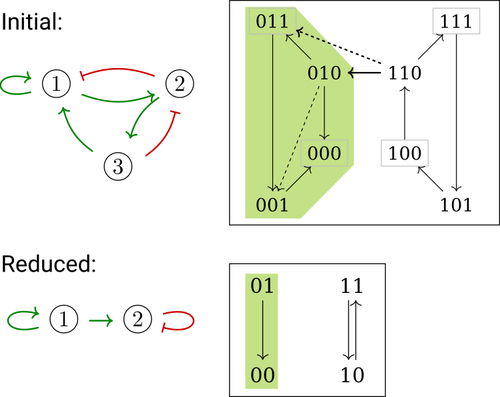
In their paper, E. Tonello and L. Paulevé [4] assess the most popular reduction that consists in eliminating a model component. Considering three typical update schemes (synchronous, asynchronous and general asynchronous updates), they thoroughly study the effects of the reduction on attractors, minimal trap spaces (minimal subspaces from which the model dynamics cannot leave), and on phenotype controls (interventions which guarantee that the dynamics ends in a phenotype defined by specific component values). Because they embody potential behaviours of the biological process under study, these are all properties of great interest for a modeller.
The authors show that eliminating a component can significantly affect some dynamical properties and may turn a control strategy ineffective. The different update schemes, targets of phenotype control and control strategies are carefully handled with useful supporting examples.
Whether the component eliminated does not share any of its regulators with its targets is shown to impact the preservation of minimal trap space. Since, in practice, model reduction amounts to eliminating several components, it would have been interesting to further explore this type of structural constraints, e.g. members of acyclical pathways or of circuits.
Overall, E. Tonello and L. Paulevé’s contribution underlines the need for caution when defining a regulatory network and characterises the consequences on critical model properties when discarding a component [4].
References
[1] Motoyosi Sugita (1963) Functional analysis of chemical systems in vivo using a logical circuit equivalent. II. The idea of a molecular automation. Journal of Theoretical Biology, 4, 179–92. https://doi.org/10.1016/0022-5193(63)90027-4
[2] Stuart Kauffman (1969) Metabolic stability and epigenesis in randomly constructed genetic nets. Journal of Theoretical Biology, 22, 437–67. https://doi.org/10.1016/0022-5193(69)90015-0
[3] René Thomas (1973) Boolean formalization of genetic control circuits. Journal of Theoretical Biology, 42, 563–85. https://doi.org/10.1016/0022-5193(73)90247-6
[4] Elisa Tonello, Loïc Paulevé (2024) Phenotype control and elimination of variables in Boolean networks. arXiv, ver.2 peer-reviewed and recommended by PCI Math Comp Biol https://arxiv.org/abs/2406.02304
The recommender in charge of the evaluation of the article and the reviewers declared that they have no conflict of interest (as defined in the code of conduct of PCI) with the authors or with the content of the article. The authors declared that they comply with the PCI rule of having no financial conflicts of interest in relation to the content of the article.
ET was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy – The Berlin Mathematics Research Center MATH+ (EXC-2046/1, project ID: 390685689). LP was funded by the French Agence Nationale pour la Recherche (ANR) in the scope of the project ``BNeDiction'' (grant number ANR-20-CE45-0001).
Evaluation round #1
DOI or URL of the preprint: https://arxiv.org/abs/2406.02304
Version of the preprint: 1
Author's Reply, 23 Jul 2024
We are very thankful to the reviewers for their comments and suggestions.
Our answers to the main points raised follow.
====================================================================
Review by David Safranek:
> The authors might think of adding some simplified scheme to explain the reductions in section 2.3 (not necessary but might help the reader to get the main point faster).
Answer: We added a figure (Figure 2) in section 2.3 to illustrate the main ideas behind the reduction method.
====================================================================
Review by Tomas Gedeon:
> - The title can be perhaps a little more specific where instead of ”and” connecting two clauses there is more specific description of the work: ”Effect of elimination of variables in Boolean networks on phenotype control” But this is just a personal preference.
Answer: We understand the idea behind the suggestion, but we prefer to keep the current title
(mainly because some results concern the reduction method first, and phenotype control only as an application).
====================================================================
> - There are two statements on page 6 close to each other that seems to say very
> similar things (if not, this should be explained):
> (1) In light of this latter remark, we restrict the analysis of control strategy be-
> haviour under reduction to the removal of components that are free in the
> control strategy.
> (2) ... it is reasonable to limit the control strategies under consideration to sub-
> spaces that do not fix any component that is fixed in the target phenotype.
Answer:
We acknowledge that this can be a source of confusion.
The first point refers to the relationship between the control strategy and the reduction,
the second to the relationship between the control strategy and the target phenotype.
We expanded the explanation around these two assumption in section 2.4.1.
We also added equations (A) and (B), to make the difference between the two conditions
hopefully more discernible.
====================================================================
> - The concept of ”linear components” on page 10 at the end of section 3.1 was
> defined and it was advertised that it will be used, but as far as I can tell, it was
> never used in the subsequent text.
Answer:
Indeed the definition of linear component does not feature in any of the results.
However, in all the examples that deal with elimination of a mediator node
we made a point of considering special mediator nodes that are also linear components.
The reason for this is that linear components are particularly "simple" intermediates
and it is quite natural to ask whether the removal of a component that has only one regulator
and one target can be considered as harmless (take for instance Saadatpour 2013 SIAM).
Therefore we wanted to highlight that, while for the validity of the conclusion of theorem 3.3
(preservation of minimal trap spaces) the restriction on linearity is not required,
in situations where the mediator hypothesis is not sufficient to guarantee preservation
of control strategies (examples 4.11, 4.13, 4.15, 4.18) adding linearity is also not sufficient.
We now made this point more explicit with a comment at the end of section 3.1
and by adding the word "linear" to all of the affected examples.
====================================================================
> Suggestion:
>
> The results seem to suggest that the trap spaces may be conceptually better objects
> than attractors, since they behave better under reductions. Trap sets (as opposed to more
> restricted trap spaces) have an analog in theory of dynamical systems where they are called
> attracting neighborhoods [1]. It is known that these sets form a lattice and that this lattice
> contains all the information about the global structure of the invariant sets.
> Although trap spaces are natural objects in the Boolean networks, it may be that the
> results for persistence of trap sets under network reduction may be stronger than or the
> trap spaces. In particular, I am curious if lattice of trap spaces is preserved under network
> reduction studied in this paper.
>
> W.D. Kalies, K. Mischaikow, and R.C.A Vandervorst. Lattice structures for attractors I. Journal of
> Computational Dynamics, I:307–338, 2014.
Answer:
We thank the reviewer for this suggestion. Indeed, the analysis of the effects of reduction
on trap spaces is not exhaustive and more aspects could be investigated in particular
in relation to the structure they form and conditions under which it is preserved.
We added a note about this point in the conclusion.
So far we could only observe that the lattice structure of trap spaces does not seem
to be preserved, in general, under reduction (even when minimal trap spaces are)
when mapping subspaces via projection.
Consider the map f(x1, x2, x3) = (x2 & x3, x1, x1) and the removal of the third component.
Since it is a mediator, Theorem 3.3 applies and the minimal trap spaces are preserved.
The reduced network is g(x1, x2) = (x1 & x2, x1).
Consider the trap spaces 0*0 and 00*.
The smallest trap space that contains both is the full space.
However, they project to 0* and 00 in the reduction, whose union is the trap space 0*, different from **.
Decision by Claudine Chaouiya , posted 12 Jul 2024, validated 12 Jul 2024
, posted 12 Jul 2024, validated 12 Jul 2024
Dear authors,
We have now received the reviewers reports, and they are quite positive. I am asking for a minor revision as you may consider their few suggestions to improve the manuscript.
Best regards
C. Chaouiya
Reviewed by Tomas Gedeon, 24 Jun 2024
Reviewed by David Safranek, 09 Jul 2024
The paper provides an extensive exploration of the impact of component reduction in Boolean networks to preservation of attractors and trap spaces forming control targets. The most important novelty is in bringing in the three update modes (synchronous, asynchronous, and general asynchronous) together with attractor-based and trap space-based phenotype control.
The authors rigorously prove situations when component-based reduction preserves existence of control strategies when going from reduced network to the original one and vice-versa. In negative cases they provide a counter example. In my view, the contribution is very relevant in the wider context of Boolean networks control and improves the formal understanding of the particular state-space reduction in that context. The computational complexity aspects targeting BN control make a well-known problem and component-based reductions provide a tool that can significantly help. In that light, the results presented in this paper are highly relevant.
The paper is consistent, it is written with good formal rigour and I have found all the proofs provided in-line to be sound and self-explainable. The content is well structured and references make a solid sample.
The authors might think of adding some simplified scheme to explain the reductions in section 2.3 (not necessary but might help the reader to get the main point faster).
I am definitely for accepting the paper as it is.
Minor comments
=============
pp2. can be answer -> can be answered
pp2. second partially -> second only partially
Title and abstract
Does the title clearly reflect the content of the article? [X] Yes
Does the abstract present the main findings of the study? [X] Yes
Introduction
Are the research questions/hypotheses/predictions clearly presented? [X] Yes,
Does the introduction build on relevant research in the field? [X] Yes
Materials and methods
Are the methods and analyses sufficiently detailed to allow replication by other researchers? [X] Yes
Results
Are the results described and interpreted correctly? [X] Yes
Discussion
Have the authors appropriately emphasized the strengths and limitations of their study/theory/methods/argument? [X] Yes
Are the conclusions adequately supported by the results (without overstating the implications of the findings)? [X] Yes










