
GEDEON Tomas
Recommendations: 0
Review: 1
Review: 1
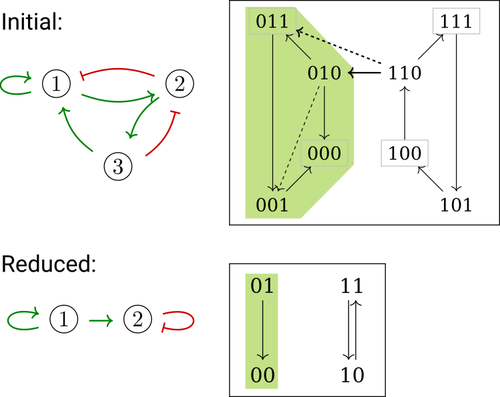
Phenotype control and elimination of variables in Boolean networks
Disclosing effects of Boolean network reduction on dynamical properties and control strategies
Recommended by Claudine Chaouiya based on reviews by Tomas Gedeon and David SafranekBoolean networks stem from seminal work by M. Sugita [1], S. Kauffman [2] and R. Thomas [3] over half a century ago. Since then, a very active field of research has been developed, leading to theoretical advances accompanied by a wealth of work on modelling genetic and signalling networks involved in a wide range of cellular processes. Boolean networks provide a successful formalism for the mathematical modelling of biological processes, with a qualitative abstraction particularly well adapted to handle the modelling of processes for which precise, quantitative data is barely available. Nevertheless, these abstract models reveal fundamental dynamical properties, such as the existence and reachability of attractors, which embody stable cellular responses (e.g. differentiated states). Analysing these properties still faces serious computational complexity. Reduction of model size was proposed as a mean to cope with this issue. Furthermore, to enhance the capacity of Boolean networks to produce relevant predictions, formal methods have been developed to systematically identify control strategies enforcing desired behaviours.
In their paper, E. Tonello and L. Paulevé [4] assess the most popular reduction that consists in eliminating a model component. Considering three typical update schemes (synchronous, asynchronous and general asynchronous updates), they thoroughly study the effects of the reduction on attractors, minimal trap spaces (minimal subspaces from which the model dynamics cannot leave), and on phenotype controls (interventions which guarantee that the dynamics ends in a phenotype defined by specific component values). Because they embody potential behaviours of the biological process under study, these are all properties of great interest for a modeller.
The authors show that eliminating a component can significantly affect some dynamical properties and may turn a control strategy ineffective. The different update schemes, targets of phenotype control and control strategies are carefully handled with useful supporting examples.
Whether the component eliminated does not share any of its regulators with its targets is shown to impact the preservation of minimal trap space. Since, in practice, model reduction amounts to eliminating several components, it would have been interesting to further explore this type of structural constraints, e.g. members of acyclical pathways or of circuits.
Overall, E. Tonello and L. Paulevé’s contribution underlines the need for caution when defining a regulatory network and characterises the consequences on critical model properties when discarding a component [4].
References
[1] Motoyosi Sugita (1963) Functional analysis of chemical systems in vivo using a logical circuit equivalent. II. The idea of a molecular automation. Journal of Theoretical Biology, 4, 179–92. https://doi.org/10.1016/0022-5193(63)90027-4
[2] Stuart Kauffman (1969) Metabolic stability and epigenesis in randomly constructed genetic nets. Journal of Theoretical Biology, 22, 437–67. https://doi.org/10.1016/0022-5193(69)90015-0
[3] René Thomas (1973) Boolean formalization of genetic control circuits. Journal of Theoretical Biology, 42, 563–85. https://doi.org/10.1016/0022-5193(73)90247-6
[4] Elisa Tonello, Loïc Paulevé (2024) Phenotype control and elimination of variables in Boolean networks. arXiv, ver.2 peer-reviewed and recommended by PCI Math Comp Biol https://arxiv.org/abs/2406.02304