
HOLLAND Barbara
- School of Natural Sciences (Mathematics), University of Tasmania, Hobart, Australia
- Evolutionary Biology, Genetics and population Genetics, Probability and statistics
- recommender
Recommendation: 1
Reviews: 2
Recommendation: 1
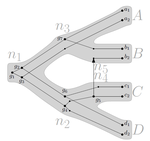
Consistency of orthology and paralogy constraints in the presence of gene transfers
Allowing gene transfers doesn't make life easier for inferring orthology and paralogy
Recommended by Barbara Holland based on reviews by 2 anonymous reviewersDetermining if genes are orthologous (i.e. homologous genes whose most common ancestor represents a speciation) or paralogous (homologous genes whose most common ancestor represents a duplication) is a foundational problem in bioinformatics. For instance, the input to almost all phylogenetic methods is a sequence alignment of genes assumed to be orthologous. Understanding if genes are paralogs or orthologs can also be important for assigning function, for example genes that have diverged following duplication may be more likely to have neofunctionalised or subfunctionalised compared to genes that have diverged following speciation, which may be more likely to have continued in a similar role.
This paper by Jones et al (2022) contributes to a wide range of literature addressing the inference of orthology/paralogy relations but takes a different approach to explaining inconsistency between an assumed species phylogeny and a relation graph (a graph where nodes represent genes and edges represent that the two genes are orthologs). Rather than assuming that inconsistencies are the result of incorrect assessment of orthology (i.e. incorrect edges in the relation graph) they ask if the relation graph could be consistent with a species tree combined with some amount of lateral (horizontal) gene transfer.
The two main questions addressed in this paper are (1) if a network N and a relation graph R are consistent, and (2) if – given a species tree S and a relation graph R – transfer arcs can be added to S in such a way that it becomes consistent with R?
The first question hinges on the concept of a reconciliation between a gene tree and a network (section 2.1) and amounts to asking if a gene tree can be found that can both be reconciled with the network and consistent with the relation graph. The authors show that the problem is NP hard. Furthermore, the related problem of attempting to find a solution using k or fewer transfers is NP-hard, and also W[1] hard implying that it is in a class of problems for which fixed parameter tractable solutions have not been found. The proof of NP hardness is by reduction to the k-multi-coloured clique problem via an intermediate problem dubbed “antichain on trees” (Section 3). The “antichain on trees” construction may be of interest to others working on algorithmic complexity with phylogenetic networks.
In the second question the possible locations of transfers are not specified (or to put it differently any time consistent transfer arc is considered possible) and it is shown that it generally will be possible to add transfer edges to S in such a way that it can be consistent with R. However, the natural extension to this question of asking if it can be done with k or fewer added arcs is also NP hard.
Many of the proofs in the paper are quite technical, but the authors have relegated a lot of this detail to the appendix thus ensuring that the main ideas and results are clear to follow in the main text. I am grateful to both reviewers for their detailed reviews and through checking of the proofs.
References
Jones M, Lafond M, Scornavacca C (2022) Consistency of orthology and paralogy constraints in the presence of gene transfers. arXiv:1705.01240 [cs], ver. 6 peer-reviewed and recommended by Peer Community in Mathematical and Computational Biology. https://arxiv.org/abs/1705.01240
Reviews: 2
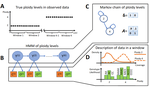
HMMploidy: inference of ploidy levels from short-read sequencing data
Detecting variation in ploidy within and between genomes
Recommended by Alan Rogers based on reviews by Barbara Holland, Benjamin Peter and Nicolas GaltierSoraggi et al. [2] describe HMMploidy, a statistical method that takes DNA sequencing data as input and uses a hidden Markov model to estimate ploidy. The method allows ploidy to vary not only between individuals, but also between and even within chromosomes. This allows the method to detect aneuploidy and also chromosomal regions in which multiple paralogous loci have been mistakenly assembled on top of one another.
HMMploidy estimates genotypes and ploidy simultaneously, with a separate estimate for each genome. The genome is divided into a series of non-overlapping windows (typically 100), and HMMploidy provides a separate estimate of ploidy within each window of each genome. The method is thus estimating a large number of parameters, and one might assume that this would reduce its accuracy. However, it benefits from large samples of genomes. Large samples increase the accuracy of internal allele frequency estimates, and this improves the accuracy of genotype and ploidy estimates. In large samples of low-coverage genomes, HMMploidy outperforms all other estimators. It does not require a reference genome of known ploidy. The power of the method increases with coverage and sample size but decreases with ploidy. Consequently, high coverage or large samples may be needed if ploidy is high.
The method is slower than some alternative methods, but run time is not excessive. Run time increases with number of windows but isn't otherwise affected by genome size. It should be feasible even with large genomes, provided that the number of windows is not too large. The authors apply their method and several alternatives to isolates of a pathogenic yeast, Cryptococcus neoformans, obtained from HIV-infected patients. With these data, HMMploidy replicated previous findings of polyploidy and aneuploidy. There were several surprises. For example, HMMploidy estimates the same ploidy in two isolates taken on different days from a single patient, even though sequencing coverage was three times as high on the later day as on the earlier one. These findings were replicated in data that were down-sampled to mimic low coverage.
Three alternative methods (ploidyNGS [1], nQuire, and nQuire.Den [3]) estimated the highest ploidy considered in all samples from each patient. The present authors suggest that these results are artifactual and reflect the wide variation in allele frequencies. Because of this variation, these methods seem to have preferred the model with the largest number of parameters. HMMploidy represents a new and potentially useful tool for studying variation in ploidy. It will be of most use in studying the genetics of asexual organisms and cancers, where aneuploidy imposes little or no penalty on reproduction. It should also be useful for detecting assembly errors in de novo genome sequences from non-model organisms.
References
[1] Augusto Corrêa dos Santos R, Goldman GH, Riaño-Pachón DM (2017) ploidyNGS: visually exploring ploidy with Next Generation Sequencing data. Bioinformatics, 33, 2575–2576. https://doi.org/10.1093/bioinformatics/btx204
[2] Soraggi S, Rhodes J, Altinkaya I, Tarrant O, Balloux F, Fisher MC, Fumagalli M (2022) HMMploidy: inference of ploidy levels from short-read sequencing data. bioRxiv, 2021.06.29.450340, ver. 6 peer-reviewed and recommended by Peer Community in Mathematical and Computational Biology. https://doi.org/10.1101/2021.06.29.450340
[3] Weiß CL, Pais M, Cano LM, Kamoun S, Burbano HA (2018) nQuire: a statistical framework for ploidy estimation using next generation sequencing. BMC Bioinformatics, 19, 122. https://doi.org/10.1186/s12859-018-2128-z
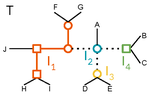
A linear time solution to the Labeled Robinson-Foulds Distance problem
Comparing reconciled gene trees in linear time
Recommended by Céline Scornavacca based on reviews by Barbara Holland, Gabriel Cardona, Jean-Baka Domelevo Entfellner and 1 anonymous reviewerUnlike a species tree, a gene tree results not only from speciation events, but also from events acting at the gene level, such as duplications and losses of gene copies, and gene transfer events [1]. The reconciliation of phylogenetic trees consists in embedding a given gene tree into a known species tree and, doing so, determining the location of these gene-level events on the gene tree [2]. Reconciled gene trees can be seen as phylogenetic trees where internal node labels are used to discriminate between different gene-level events. Comparing them is of foremost importance in order to assess the performance of various reconciliation methods (e.g. [3]).
A paper describing an extension of the widely used Robinson-Foulds (RF) distance [4] to trees with labeled internal nodes was presented earlier this year [5]. This distance, called ELRF, is based on edge edits and coincides with the RF distance when all internal labels are identical; unfortunately, the ELRF distance is very costly to compute. In the present paper [6], the authors introduce a distance called LRF, which is inspired by the TED (Tree Edit Distance [7]) and is based on node edits. As the ELRF, the new distance coincides with the RF distance for identically-labeled internal nodes, but has the additional desirable features of being computable in linear time. Also, in the ELRF distance, an edge can be deleted if only it connects nodes with the same label. The new formulation does not have this restriction, and this is, in my opinion, an improvement since the restriction makes little sense in the comparison of reconciled gene trees.
The authors show the pertinence of this new distance by studying the impact of taxon sampling on reconciled gene trees when internal labels are computed via a method based on species overlap. The linear algorithm to compute the LRF distance presented in the paper has been implemented and the software —written in Python— is freely available for the community to use it. I bet that the LRF distance will be widely used in the coming years!
References
[1] Maddison, W. P. (1997). Gene trees in species trees. Systematic biology, 46(3), 523-536. doi: https://doi.org/10.1093/sysbio/46.3.523
[2] Boussau, B., and Scornavacca, C. (2020). Reconciling gene trees with species trees. Phylogenetics in the Genomic Era, p. 3.2:1–3.2:23.
[3] Doyon, J. P., Chauve, C., and Hamel, S. (2009). Space of gene/species trees reconciliations and parsimonious models. Journal of Computational Biology, 16(10), 1399-1418. doi: https://doi.org/10.1089/cmb.2009.0095
[4] Robinson, D. F., and Foulds, L. R. (1981). Comparison of phylogenetic trees. Mathematical biosciences, 53(1-2), 131-147. doi: https://doi.org/10.1016/0025-5564(81)90043-2
[5] Briand, B., Dessimoz, C., El-Mabrouk, N., Lafond, M. and Lobinska, G. (2020). A generalized Robinson-Foulds distance for labeled trees. BMC Genomics 21, 779. doi: https://doi.org/10.1186/s12864-020-07011-0
[6] Briand, S., Dessimoz, C., El-Mabrouk, N. and Nevers, Y. (2020) A linear time solution to the labeled Robinson-Foulds distance problem. bioRxiv, 2020.09.14.293522, ver. 4 peer-reviewed and recommended by PCI Mathematical and Computational Biology. doi: https://doi.org/10.1101/2020.09.14.293522
[7] Zhang, K., and Shasha, D. (1989). Simple fast algorithms for the editing distance between trees and related problems. SIAM journal on computing, 18(6), 1245-1262. doi: https://doi.org/10.1137/0218082