Latest recommendations

| Id | Title | Authors | Abstract | Picture | Thematic fields▼ | Recommender | Reviewers | Submission date | |
|---|---|---|---|---|---|---|---|---|---|
21 Feb 2022
Consistency of orthology and paralogy constraints in the presence of gene transfersMark Jones, Manuel Lafond, Celine Scornavacca https://arxiv.org/abs/1705.01240Allowing gene transfers doesn't make life easier for inferring orthology and paralogyRecommended by Barbara Holland based on reviews by 2 anonymous reviewersDetermining if genes are orthologous (i.e. homologous genes whose most common ancestor represents a speciation) or paralogous (homologous genes whose most common ancestor represents a duplication) is a foundational problem in bioinformatics. For instance, the input to almost all phylogenetic methods is a sequence alignment of genes assumed to be orthologous. Understanding if genes are paralogs or orthologs can also be important for assigning function, for example genes that have diverged following duplication may be more likely to have neofunctionalised or subfunctionalised compared to genes that have diverged following speciation, which may be more likely to have continued in a similar role. This paper by Jones et al (2022) contributes to a wide range of literature addressing the inference of orthology/paralogy relations but takes a different approach to explaining inconsistency between an assumed species phylogeny and a relation graph (a graph where nodes represent genes and edges represent that the two genes are orthologs). Rather than assuming that inconsistencies are the result of incorrect assessment of orthology (i.e. incorrect edges in the relation graph) they ask if the relation graph could be consistent with a species tree combined with some amount of lateral (horizontal) gene transfer. The two main questions addressed in this paper are (1) if a network N and a relation graph R are consistent, and (2) if – given a species tree S and a relation graph R – transfer arcs can be added to S in such a way that it becomes consistent with R? The first question hinges on the concept of a reconciliation between a gene tree and a network (section 2.1) and amounts to asking if a gene tree can be found that can both be reconciled with the network and consistent with the relation graph. The authors show that the problem is NP hard. Furthermore, the related problem of attempting to find a solution using k or fewer transfers is NP-hard, and also W[1] hard implying that it is in a class of problems for which fixed parameter tractable solutions have not been found. The proof of NP hardness is by reduction to the k-multi-coloured clique problem via an intermediate problem dubbed “antichain on trees” (Section 3). The “antichain on trees” construction may be of interest to others working on algorithmic complexity with phylogenetic networks. In the second question the possible locations of transfers are not specified (or to put it differently any time consistent transfer arc is considered possible) and it is shown that it generally will be possible to add transfer edges to S in such a way that it can be consistent with R. However, the natural extension to this question of asking if it can be done with k or fewer added arcs is also NP hard. Many of the proofs in the paper are quite technical, but the authors have relegated a lot of this detail to the appendix thus ensuring that the main ideas and results are clear to follow in the main text. I am grateful to both reviewers for their detailed reviews and through checking of the proofs. References Jones M, Lafond M, Scornavacca C (2022) Consistency of orthology and paralogy constraints in the presence of gene transfers. arXiv:1705.01240 [cs], ver. 6 peer-reviewed and recommended by Peer Community in Mathematical and Computational Biology. https://arxiv.org/abs/1705.01240 | Consistency of orthology and paralogy constraints in the presence of gene transfers | Mark Jones, Manuel Lafond, Celine Scornavacca | <p style="text-align: justify;">Orthology and paralogy relations are often inferred by methods based on gene sequence similarity that yield a graph depicting the relationships between gene pairs. Such relation graphs frequently contain errors, as ... |  | Computational complexity, Design and analysis of algorithms, Evolutionary Biology, Graph theory | Barbara Holland | 2021-06-30 15:01:44 | View | |
10 Apr 2024
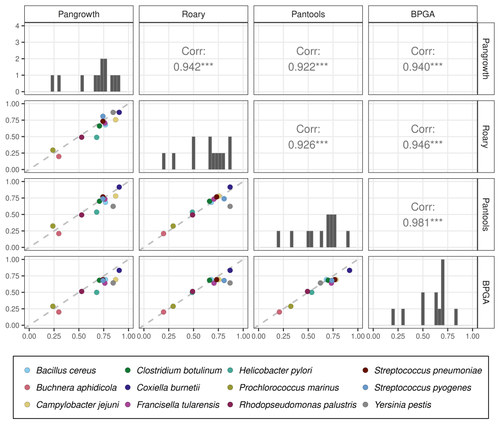
Revisiting pangenome openness with k-mersLuca Parmigiani, Roland Wittler, Jens Stoye https://doi.org/10.1101/2022.11.15.516472Faster method for estimating the openness of speciesRecommended by Leo van Iersel based on reviews by Guillaume Marçais, Abiola Akinnubi and 1 anonymous reviewerWhen sequencing more and more genomes of a species (or a group of closely related species), a natural question to ask is how quickly the total number of distinct sequences grows as a function of the total number of sequenced genomes. A similar question can be asked about the number of distinct genes or the number of distinct k-mers (length-k subsequences). References [1] Parmigiani L., Wittler, R. and Stoye, J. (2024) "Revisiting pangenome openness with k-mers". bioRxiv, ver. 4 peer-reviewed and recommended by Peer Community In Mathematical and Computational Biology. https://doi.org/10.1101/2022.11.15.516472 | Revisiting pangenome openness with k-mers | Luca Parmigiani, Roland Wittler, Jens Stoye | <p style="text-align: justify;">Pangenomics is the study of related genomes collectively, usually from the same species or closely related taxa. Originally, pangenomes were defined for bacterial species. After the concept was extended to eukaryoti... |  | Combinatorics, Genomics and Transcriptomics | Leo van Iersel | Guillaume Marçais, Yadong Zhang | 2022-11-22 14:48:18 | View |
26 May 2021
An efficient algorithm for estimating population history from genetic dataAlan R. Rogers https://doi.org/10.1101/2021.01.23.427922An efficient implementation of legofit software to infer demographic histories from population genetic dataRecommended by Matteo Fumagalli based on reviews by Fernando Racimo and 1 anonymous reviewer based on reviews by Fernando Racimo and 1 anonymous reviewer
The estimation of demographic parameters from population genetic data has been the subject of many scientific studies [1]. Among these efforts, legofit was firstly proposed in 2019 as a tool to infer size changes, subdivision and gene flow events from patterns of nucleotidic variation [2]. The first release of legofit used a stochastic algorithm to fit population parameters to the observed data. As it requires simulations to evaluate the fitting of each model, it is computationally intensive and can only be deployed on high-performance computing clusters. To overcome this issue, Rogers proposes a new implementation of legofit based on a deterministic algorithm that allows the estimation of demographic histories to be computationally faster and more accurate [3]. The new algorithm employs a continuous-time Markov chain that traces the ancestry of each sample into the past. The calculations are now divided into two steps, the first one being solved numerically. To test the hypothesis that the new implementation of legofit produces a more desirable performance, Rogers generated extensive simulations of genomes from African, European, Neanderthal and Denisovan populations with msprime [4]. Additionally, legofit was tested on real genetic data from samples of said populations, following a previously published study [5]. Based on simulations, the new deterministic algorithm is more than 1600 times faster than the previous stochastic model. Notably, the new version of legofit produces smaller residual errors, although the overall accuracy to estimate population parameters is comparable to the one obtained using the stochastic algorithm. When applied to real data, the new implementation of legofit was able to recapitulate previous findings of a complex demographic model with early gene flow from humans to Neanderthal [5]. Notably, the new implementation generates better discrimination between models, therefore leading to a better precision at predicting the population history. Some parameters estimated from real data point towards unrealistic scenarios, suggesting that the initial model could be misspecified. Further research is needed to fully explore the parameter range that can be evaluated by legofit, and to clarify the source of any associated bias. Additionally, the inclusion of data uncertainty in parameter estimation and model selection may be required to apply legofit to low-coverage high-throughput sequencing data [6]. Nevertheless, legofit is an efficient, accessible and user-friendly software to infer demographic parameters from genetic data and can be widely applied to test hypotheses in evolutionary biology. The new implementation of legofit software is freely available at https://github.com/alanrogers/legofit. References [1] Spence JP, Steinrücken M, Terhorst J, Song YS (2018) Inference of population history using coalescent HMMs: review and outlook. Current Opinion in Genetics & Development, 53, 70–76. https://doi.org/10.1016/j.gde.2018.07.002 [2] Rogers AR (2019) Legofit: estimating population history from genetic data. BMC Bioinformatics, 20, 526. https://doi.org/10.1186/s12859-019-3154-1 [3] Rogers AR (2021) An Efficient Algorithm for Estimating Population History from Genetic Data. bioRxiv, 2021.01.23.427922, ver. 5 peer-reviewed and recommended by Peer community in Mathematical and Computational Biology. https://doi.org/10.1101/2021.01.23.427922 [4] Kelleher J, Etheridge AM, McVean G (2016) Efficient Coalescent Simulation and Genealogical Analysis for Large Sample Sizes. PLOS Computational Biology, 12, e1004842. https://doi.org/10.1371/journal.pcbi.1004842 [5] Rogers AR, Harris NS, Achenbach AA (2020) Neanderthal-Denisovan ancestors interbred with a distantly related hominin. Science Advances, 6, eaay5483. https://doi.org/10.1126/sciadv.aay5483 [6] Soraggi S, Wiuf C, Albrechtsen A (2018) Powerful Inference with the D-Statistic on Low-Coverage Whole-Genome Data. G3 Genes|Genomes|Genetics, 8, 551–566. https://doi.org/10.1534/g3.117.300192 | An efficient algorithm for estimating population history from genetic data | Alan R. Rogers | <p style="text-align: justify;">The Legofit statistical package uses genetic data to estimate parameters describing population history. Previous versions used computer simulations to estimate probabilities, an approach that limited both speed and ... |  | Combinatorics, Genetics and population Genetics | Matteo Fumagalli | 2021-01-26 20:04:35 | View | |
12 Oct 2023
When Three Trees Go to WarLeo van Iersel and Mark Jones and Mathias Weller https://hal.science/hal-04013152v3Bounding the reticulation number for three phylogenetic treesRecommended by Simone Linz based on reviews by Guillaume Scholz and Stefan GrünewaldReconstructing a phylogenetic network for a set of conflicting phylogenetic trees on the same set of leaves remains an active strand of research in mathematical and computational phylogenetic since 2005, when Baroni et al. [1] showed that the minimum number of reticulations h(T,T') needed to simultaneously embed two rooted binary phylogenetic trees T and T' into a rooted binary phylogenetic network is one less than the size of a maximum acyclic agreement forest for T and T'. In the same paper, the authors showed that h(T,T') is bounded from above by n-2, where n is the number of leaves of T and T' and that this bound is sharp. That is, for a fixed n, there exist two rooted binary phylogenetic trees T and T' such that h(T,T')=n-2. Since 2005, many papers have been published that develop exact algorithms and heuristics to solve the above NP-hard minimisation problem in practice, which is often referred to as Minimum Hybridisation in the literature, and that further investigate the mathematical underpinnings of Minimum Hybridisation and related problems. However, many such studies are restricted to two trees and much less is known about Minimum Hybridisation for when the input consists of more than two phylogenetic trees, which is the more relevant cases from a biological point of view. In [2], van Iersel, Jones, and Weller establish the first lower bound for the minimum reticulation number for more than two rooted binary phylogenetic trees, with a focus on exactly three trees. The above-mentioned connection between the minimum number of reticulations and maximum acyclic agreement forests does not extend to three (or more) trees. Instead, to establish their result, the authors use multi-labelled trees as an intermediate structure between phylogenetic trees and phylogenetic networks to show that, for each ε>0, there exist three caterpillar trees on n leaves such that any phylogenetic network that simultaneously embeds these three trees has at least (3/2 - ε)n reticulations. Perhaps unsurprising, caterpillar trees were also used by Baroni et al. [1] to establish that their upper bound on h(T,T') is sharp. Structurally, these trees have the property that each internal vertex is adjacent to a leaf. Each caterpillar tree can therefore be viewed as a sequence of characters, and it is exactly this viewpoint that is heavily used in [2]. More specifically, sequences with short common subsequences correspond to caterpillar trees that need many reticulations when embedded in a phylogenetic network. It would consequently be interesting to further investigate connections between caterpillar trees and certain types of sequences. Can they be used to shed more light on bounds for the minimum reticulation number? References [1] Baroni, M., Grünewald, S., Moulton, V., and Semple, C. (2005) "Bounding the number of hybridisation events for a consistent evolutionary history". J. Math. Biol. 51, 171–182. https://doi.org/10.1007/s00285-005-0315-9 | When Three Trees Go to War | Leo van Iersel and Mark Jones and Mathias Weller | <p style="text-align: justify;">How many reticulations are needed for a phylogenetic network to display a given set of k phylogenetic trees on n leaves? For k = 2, Baroni, Semple, and Steel [Ann. Comb. 8, 391-408 (2005)] showed that the answer is ... |  | Combinatorics, Evolutionary Biology, Graph theory | Simone Linz | 2023-03-07 18:49:21 | View | |
24 Dec 2020
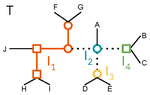
A linear time solution to the Labeled Robinson-Foulds Distance problemSamuel Briand, Christophe Dessimoz, Nadia El-Mabrouk and Yannis Nevers https://doi.org/10.1101/2020.09.14.293522Comparing reconciled gene trees in linear timeRecommended by Céline Scornavacca based on reviews by Barbara Holland, Gabriel Cardona, Jean-Baka Domelevo Entfellner and 1 anonymous reviewer based on reviews by Barbara Holland, Gabriel Cardona, Jean-Baka Domelevo Entfellner and 1 anonymous reviewer
Unlike a species tree, a gene tree results not only from speciation events, but also from events acting at the gene level, such as duplications and losses of gene copies, and gene transfer events [1]. The reconciliation of phylogenetic trees consists in embedding a given gene tree into a known species tree and, doing so, determining the location of these gene-level events on the gene tree [2]. Reconciled gene trees can be seen as phylogenetic trees where internal node labels are used to discriminate between different gene-level events. Comparing them is of foremost importance in order to assess the performance of various reconciliation methods (e.g. [3]). References [1] Maddison, W. P. (1997). Gene trees in species trees. Systematic biology, 46(3), 523-536. doi: https://doi.org/10.1093/sysbio/46.3.523 | A linear time solution to the Labeled Robinson-Foulds Distance problem | Samuel Briand, Christophe Dessimoz, Nadia El-Mabrouk and Yannis Nevers | <p>Motivation Comparing trees is a basic task for many purposes, and especially in phylogeny where different tree reconstruction tools may lead to different trees, likely representing contradictory evolutionary information. While a large variety o... |  | Combinatorics, Design and analysis of algorithms, Evolutionary Biology | Céline Scornavacca | 2020-08-20 21:06:23 | View | |
18 Sep 2023
Minimal encodings of canonical k-mers for general alphabets and even k-mer sizesRecommended by Paul Medvedev based on reviews by 2 anonymous reviewersAs part of many bioinformatics tools, one encodes a k-mer, which is a string, into an integer. The natural encoding uses a bijective function to map the k-mers onto the interval [0, s^k - ], where s is the alphabet size. This encoding is minimal, in the sense that the encoded integer ranges from 0 to the number of represented k-mers minus 1. However, often one is only interested in encoding canonical k-mers. One common definition is that a k-mer is canonical if it is lexicographically not larger than its reverse complement. In this case, only about half the k-mers from the universe of k-mers are canonical, and the natural encoding is no longer minimal. For the special case of a DNA alphabet and odd k, there exists a "parity-based" encoding for canonical k-mers which is minimal. In [1], the author presents a minimal encoding for canonical k-mers that works for general alphabets and both odd and even k. They also give an efficient bit-based representation for the DNA alphabet. This paper fills a theoretically interesting and often overlooked gap in how to encode k-mers as integers. It is not yet clear what practical applications this encoding will have, as the author readily acknowledges in the manuscript. Neither the author nor the reviewers are aware of any practical situations where the lack of a minimal encoding "leads to serious limitations." However, even in an applied field like bioinformatics, it would be short-sighted to only value theoretical work that has an immediate application; often, the application is several hops away and not apparent at the time of the original work. In fact, I would speculate that there may be significant benefits reaped if there was more theoretical attention paid to the fact that k-mers are often restricted to be canonical. Many papers in the field sweep under the rug the fact that k-mers are made canonical, leaving it as an implementation detail. This may indicate that the theory to describe and analyze this situation is underdeveloped. This paper makes a step forward to develop this theory, and I am hopeful that it may lead to substantial practical impact in the future. References [1] Roland Wittler (2023) "General encoding of canonical k-mers. bioRxiv, ver.2, peer-reviewed and recommended by Peer Community in Mathematical and Computational Biology https://doi.org/10.1101/2023.03.09.531845 | General encoding of canonical *k*-mers | Roland Wittler | <p style="text-align: justify;">To index or compare sequences efficiently, often <em>k</em>-mers, i.e., substrings of fixed length <em>k</em>, are used. For efficient indexing or storage, <em>k</em>-mers are encoded as integers, e.g., applying som... |  | Combinatorics, Computational complexity, Genomics and Transcriptomics | Paul Medvedev | Anonymous | 2023-03-13 17:01:37 | View |
14 Mar 2023

Marker and source-marker reprogramming of Most Permissive Boolean networks and ensembles with BoNesisLoïc Paulevé https://doi.org/10.48550/arXiv.2207.13307Reprogramming of locally-monotone Boolean networks with BoNesisRecommended by Sergiu Ivanov based on reviews by Ismail Belgacem and 1 anonymous reviewerReprogramming of cellular networks is a well known challenge in computational biology consisting first of all in properly representing an ensemble of networks having a role in a phenomenon of interest, and secondly in designing strategies to alter the functioning of this ensemble in the desired direction. Important applications involve disease study: a therapy can be seen as a reprogramming strategy, and the disease itself can be considered a result of a series of adversarial reprogramming actions. The origins of this domain go back to the seminal paper by Barabási et al. [1] which formalized the concept of network medicine. An abstract tool which has gathered considerable success in network medicine and network biology are Boolean networks: sets of Boolean variables, each equipped with a Boolean update function describing how to compute the next value of the variable from the values of the other variables. Despite apparent dissimilarity with the biological systems which involve varying quantities and continuous processes, Boolean networks have been very effective in representing biological networks whose entities are typically seen as being on or off. Particular examples are protein signalling networks as well as gene regulatory networks. The paper [2] by Loïc Paulevé presents a versatile tool for tackling reprogramming of Boolean networks seen as models of biological networks. The problem of reprogramming is often formulated as the problem of finding a set of perturbations which guarantee some properties on the attractors. The work [2] relies on the most permissive semantics [3], which together with the modelling assumption allows for considerable speed-up in the practically relevant subclass of locally-monotone Boolean networks. The paper is structured as a tutorial. It starts by introducing the formalism, defining 4 different general variants of reprogramming under the most permissive semantics, and presenting evaluations of their complexity in terms of the polynomial hierarchy. The author then describes the software tool BoNesis which can handle different problems related to Boolean networks, and in particular the 4 reprogramming variants. The presentation includes concrete code examples with their output, which should be very helpful for future users. The paper [2] introduces a novel scenario: reprogramming of ensembles of Boolean networks delineated by some properties, including for example the property of having a given interaction graph. Ensemble reprogramming looks particularly promising in situations in which the biological knowledge is insufficient to fully determine all the update functions, i.e. in the majority of modelling situations. Finally, the author also shows how BoNesis can be used to deal with sequential reprogramming, which is another promising direction in computational controllability, potentially enabling more efficient therapies [4,5]. REFERENCES
| Marker and source-marker reprogramming of Most Permissive Boolean networks and ensembles with BoNesis | Loïc Paulevé | <p style="text-align: justify;">Boolean networks (BNs) are discrete dynamical systems with applications to the modeling of cellular behaviors. In this paper, we demonstrate how the software BoNesis can be employed to exhaustively identify combinat... |  | Combinatorics, Computational complexity, Dynamical systems, Molecular Biology, Systems biology | Sergiu Ivanov | Ismail Belgacem, Anonymous | 2022-08-31 15:00:21 | View |
07 Sep 2021

The origin of the allometric scaling of lung ventilation in mammalsFrédérique Noël, Cyril Karamaoun, Jerome A. Dempsey, Benjamin Mauroy https://arxiv.org/abs/2005.12362How mammals adapt their breath to body activity – and how this depends on body sizeRecommended by Wolfram Liebermeister based on reviews by Elad Noor, Oliver Ebenhöh, Stefan Schuster and Megumi InoueHow fast and how deep do animals breathe, and how does this depend on how active they are? To answer this question, one needs to dig deeply into how breathing works and what biophysical processes it involves. And one needs to think about body size. It is impressive how nature adapts the same body plan – e.g. the skeletal structure of mammals – to various shapes and sizes. From mice to whales, also the functioning of most organs remains the same; they are just differently scaled. Scaling does not just mean “making bigger or smaller”. As already noted by Galilei, body shapes change as they are adapted to body dimensions, and the same holds for physiological variables. Many such variables, for instance, heartbeat rates, follow scaling laws of the form y~x^a, where x denotes body mass and the exponent a is typically a multiple of ¼ [1]. These unusual exponents – instead of multiples of ⅓, which would be expected from simple geometrical scaling – are why these laws are called “allometric”. Kleiber’s law for metabolic rates, with a scaling exponent of ¾, is a classic example [2]. As shown by G. West, allometric laws can be explained through a few simple steps [1]. In his models, he focused on network-like organs such as the vascular system and assumed that these systems show a self-similar structure, with a fixed minimal unit (for instance, capillaries) but varying numbers of hierarchy levels depending on body size. To determine the flow through such networks, he employed biophysical models and optimality principles (for instance, assuming that oxygen must be transported at a minimal mechanical effort), and showed that the solutions – and the physiological variables – respect the known scaling relations. The paper “The origin of the allometric scaling of lung ventilation in mammals“ by Noël et al. [3], applies this thinking to the depth and rate of breathing in mammals. Scaling laws describing breathing in resting animals have been known since the 1950s [4], with exponents of 1 (for tidal volume) and -¼ (for breathing frequency). Equipped with a detailed biophysical model, Noël et al. revisit this question, extending these laws to other metabolic regimes. Their starting point is a model of the human lung, developed previously by two of the authors [5], which assumes that we meet our oxygen demand with minimal lung movements. To state this as an optimization problem, the model combines two submodels: a mechanical model describing the energetic effort of ventilation and a highly detailed model of convection and diffusion in self-similar lung geometries. Breathing depths and rates are computed by numerical optimization, and to obtain results for mammals of any size many of the model parameters are described by known scaling laws. As expected, the depth of breathing (measured by tidal volume) scales almost proportionally with body mass and increases with metabolic demand, while the breathing rate decreases with body mass, with an exponent of about -¼. However, the laws for the breathing rate hold only for basal activity; at higher metabolic rates, which are modeled here for the first time, the exponent deviates strongly from this value, in line with empirical data. Why is this paper important? The authors present a highly complex model of lung physiology that integrates a wide range of biophysical details and passes a difficult test: the successful prediction of unexplained scaling exponents. These scaling relations may help us transfer insights from animal models to humans and in reverse: data for breathing during exercise, which are easy to measure in humans, can be extrapolated to other species. Aside from the scaling laws, the model also reveals physiological mechanisms. In the larger lung branches, oxygen is transported mainly by air movement (convection), while in smaller branches air flow is slow and oxygen moves by diffusion. The transition between these regimes can occur at different depths in the lung: as the authors state, “the localization of this transition determines how ventilation should be controlled to minimize its energetic cost at any metabolic regime”. In the model, the optimal location for the transition depends on oxygen demand [5, 6]: the transition occurs deeper in the lung in exercise regimes than at rest, allowing for more oxygen to be taken up. However, the effects of this shift depend on body size: while small mammals generally use the entire exchange surface of their lungs, large mammals keep a reserve for higher activities, which becomes accessible as their transition zone moves at high metabolic rates. Hence, scaling can entail qualitative differences between species! Altogether, the paper shows how the dynamics of ventilation depend on lung morphology. But this may also play out in the other direction: if energy-efficient ventilation depends on body activity, and therefore on ecological niches, a niche may put evolutionary pressures on lung geometry. Hence, by understanding how deep and fast animals breathe, we may also learn about how behavior, physiology, and anatomy co-evolve. References [1] West GB, Brown JH, Enquist BJ (1997) A General Model for the Origin of Allometric Scaling Laws in Biology. Science 276 (5309), 122–126. https://doi.org/10.1126/science.276.5309.122 [2] Kleiber M (1947) Body size and metabolic rate. Physiological Reviews, 27, 511–541. https://doi.org/10.1152/physrev.1947.27.4.511 [3] Noël F., Karamaoun C., Dempsey J. A. and Mauroy B. (2021) The origin of the allometric scaling of lung's ventilation in mammals. arXiv, 2005.12362, ver. 6 peer-reviewed and recommended by Peer community in Mathematical and Computational Biology. https://arxiv.org/abs/2005.12362 [4] Otis AB, Fenn WO, Rahn H (1950) Mechanics of Breathing in Man. Journal of Applied Physiology, 2, 592–607. https://doi.org/10.1152/jappl.1950.2.11.592 [5] Noël F, Mauroy B (2019) Interplay Between Optimal Ventilation and Gas Transport in a Model of the Human Lung. Frontiers in Physiology, 10, 488. https://doi.org/10.3389/fphys.2019.00488 [6] Sapoval B, Filoche M, Weibel ER (2002) Smaller is better—but not too small: A physical scale for the design of the mammalian pulmonary acinus. Proceedings of the National Academy of Sciences, 99, 10411–10416. https://doi.org/10.1073/pnas.122352499 | The origin of the allometric scaling of lung ventilation in mammals | Frédérique Noël, Cyril Karamaoun, Jerome A. Dempsey, Benjamin Mauroy | <p>A model of optimal control of ventilation has recently been developed for humans. This model highlights the importance of the localization of the transition between a convective and a diffusive transport of respiratory gas. This localization de... |  | Biophysics, Evolutionary Biology, Physiology | Wolfram Liebermeister | 2020-08-28 15:18:03 | View | |
26 Feb 2024

A workflow for processing global datasets: application to intercroppingRémi Mahmoud, Pierre Casadebaig, Nadine Hilgert, Noémie Gaudio https://hal.science/hal-04145269Collecting, assembling and sharing data in crop sciencesRecommended by Eric Tannier based on reviews by Christine Dillmann and 2 anonymous reviewers based on reviews by Christine Dillmann and 2 anonymous reviewers
It is often the case that scientific knowledge exists but is scattered across numerous experimental studies. Because of this dispersion in different formats, it remains difficult to access, extract, reproduce, confirm or generalise. This is the case in crop science, where Mahmoud et al [1] propose to collect and assemble data from numerous field experiments on intercropping. It happens that the construction of the global dataset requires a lot of time, attention and a well thought-out method, inspired by the literature on data science [2] and adapted to the specificities of crop science. This activity also leads to new possibilities that were not available in individual datasets, such as the detection of full factorial designs using graph theory tools developed on top of the global dataset. The study by Mahmoud et al [1] has thus multiple dimensions:
I was particularly interested in the promotion of the FAIR principles, perhaps used a little too uncritically in my view, as an obvious solution to data sharing. On the one hand, I am admiring and grateful for the availability of these data, some of which have never been published, nor associated with published results. This approach is likely to unearth buried treasures. On the other hand, I can understand the reluctance of some data producers to commit to total, definitive sharing, facilitating automatic reading, without having thought about a certain reciprocity on the part of users and use by artificial intelligence. Reciprocity in terms of recognition, as is discussed by Mahmoud et al [1], but also in terms of contribution to the commons [5] or reading conditions for machine learning. References [1] Mahmoud R., Casadebaig P., Hilgert N., Gaudio N. A workflow for processing global datasets: application to intercropping. 2024. ⟨hal-04145269v2⟩ ver. 2 peer-reviewed and recommended by Peer Community in Mathematical and Computational Biology. https://hal.science/hal-04145269 [2] Wickham, H. 2014. Tidy data. Journal of Statistical Software 59(10) https://doi.org/10.18637/jss.v059.i10 [3] Gaudio, N., R. Mahmoud, L. Bedoussac, E. Justes, E.-P. Journet, et al. 2023. A global dataset gathering 37 field experiments involving cereal-legume intercrops and their corresponding sole crops. https://doi.org/10.5281/zenodo.8081577 [4] Mahmoud, R., Casadebaig, P., Hilgert, N. et al. Species choice and N fertilization influence yield gains through complementarity and selection effects in cereal-legume intercrops. Agron. Sustain. Dev. 42, 12 (2022). https://doi.org/10.1007/s13593-022-00754-y [5] Bernault, C. « Licences réciproques » et droit d'auteur : l'économie collaborative au service des biens communs ?. Mélanges en l'honneur de François Collart Dutilleul, Dalloz, pp.91-102, 2017, 978-2-247-17057-9. https://shs.hal.science/halshs-01562241 | A workflow for processing global datasets: application to intercropping | Rémi Mahmoud, Pierre Casadebaig, Nadine Hilgert, Noémie Gaudio | <p>Field experiments are a key source of data and knowledge in agricultural research. An emerging practice is to compile the measurements and results of these experiments (rather than the results of publications, as in meta-analysis) into global d... |  | Agricultural Science | Eric Tannier | 2023-06-29 15:38:28 | View |
MANAGING BOARD
Caroline Colijn
Christophe Dessimoz
Barbara Holland
Hirohisa Kishino
Anita Layton
Wolfram Liebermeister
Christian Robert
Celine Scornavacca
Donate Weghorn










